بحث عن الدوال الرئيسة الام والتحويلات الهندسية

بحث عن الدوال الرئيسة الام والتحويلات الهندسية من الأبحاث المهمة التي ترتبط ارتباطًا وثيقًا بدراسة الدوال وكيفية تحليلها وتمثيلها تمثيلًا بيانيًا، وتعلم هذا الموضوع من الأمور التي تيسر على الطالب فهم تكوين الدوال والرسوم البيانية؛ حيث إن الاختلاف بينها يكون ناتجًا عن التحويلات الهندسية المختلفة. وفي هذا المقال من موقع المرجع سوف ندرج لكم بحث عن الدوال الرئيسة الأم والتحويلات الهندسية يشمل تعريف هذه الدوال الأم وبيان خصائصها، بالإضافة إلى توضيح التحويلات الهندسية وتأثيرها.

مقدمة بحث عن الدوال الرئيسة الام والتحويلات الهندسية

بسم الله الرحمن الرحيم، والحمد لله رب العالمين؛ له الحمد حمدًا طيبًا مباركًا يليق بجلال وجهه وعظيم سلطانه، والصلاة والسلام على سيدنا محمد المعلم والهادي والمرشد وعلى آله وأصحابه أجمعين، أما بعد:

أقدم بحثي هذا عن واحد من أهم الموضوعات في علم الرياضيات، وهو الدوال الرئيسة الأم والتحويلات الهندسية التي تجري عليها، حيث يعد هذا الموضوع ذا أهمية بالغة يجب تسليط الضوء عليها، لأنه يسهل على العلماء والدارسين والطلاب بمستوياتهم المختلفة فهم كيفية تكوين الدوال المختلفة، والتمثيل البياني لها وما يؤثر عليها من العمليات الحسابية فيؤدي إلى تغير مكانها أو شكلها على المستوى البياني حسب العملية التي يتم إجراؤها.

فهم التحويلات الهندسية يساعد على بناء التطبيقات والبرامج التي تساعد أصحاب الشركات والمؤسسات على عمل المخططات التي تبين مجريات الأحداث؛ مثل دراسة تخفيض سعر البيع على إجمالي الربح، أو دراسة تأثير خسارة معينة على عائدات الشركة، وغير ذلك.

شاهد أيضًا: بحث عن الدوال وأنواعها كامل

بحث عن الدوال الرئيسة الام والتحويلات الهندسية

سوف أبدأ في هذا البحث بذكر تعريف الدوال الرئيسية الأم وبيان أنواعها بشكل إجمالي، ومن ثم سوف أفصل في أنواع الدوال الرئيسة وصيغها القياسية، وبيان الدالة الأم لكل منها، مع توضيح طريقة رسمها بشكل مبسط. بعد ذلك بيان خصائص الدوال الرئيسية الأم، والتحويلات الهندسية التي تجري عليها بالترتيب، بحيث سوف يكون ترتيب الموضوعات كما يأتي:

• الباب الأول: تعريف الدوال الرئيسة الأم وأنواعها؛ الدالة الثابتة، الدالة الخطية الأم، الدالة التربيعية الأم، الدالة الجذر التربيعي الأم، الدالة النسبية الأم، الدالة الدرجية الأم، دالة القيمة المطلقة الأم.
• الباب الثاني: خصائص الدالة الرئيسية الأم
• الباب الثالث: تعريف التحويلات الهندسية على الدوال الأم
• الباب الرابع: أنواع التحويلات الهندسية على الدوال
  • المطلب الأول: انسحاب الدوال الرئيسية الأم: الانسحاب الرأسي للدوال، والانسحاب الأفقي للدوال.
  • المطلب الثاني: الانعكاس حول المحورين الاحداثيين للدوال الرئيسية الأم: الانعكاس حول المحور السيني، والانعكاس حول المحور الصادي.
  • المطلب الثالث: تمدد الدوال الرئيسية الأم: التمدد الرأسي للدوال، والتمدد الأفقي للدوال
• الباب الخامس: التحويلات الهندسية مع دوال القيمة المطلقة

شاهد أيضًا: بحث عن علم الرياضيات

تعريف الدوال الرئيسة الام

تتكون الدوال من عائلات مختلفة وهذه العائلات تشترك فيما بينها بالصفات والخصائص، وفي كل عائلة هناك دالة تعرف بالدالة الرئيسية الأم باعتبارها الدالة الأبسط في العائلة ومن خلال إجراء التحويلات الهندسية عليها يمكننا إيجاد بقية دوال العائلة. وهذا بالتأكيد ينعكس على التمثيل البياني لها من خلال ما يحدث له من الإزاحة والتمدد والانعكاس ونحو ذلك من الأمور التي تختلف وفقًا لما يجري عليها من العمليات.

الدالة الثابتة

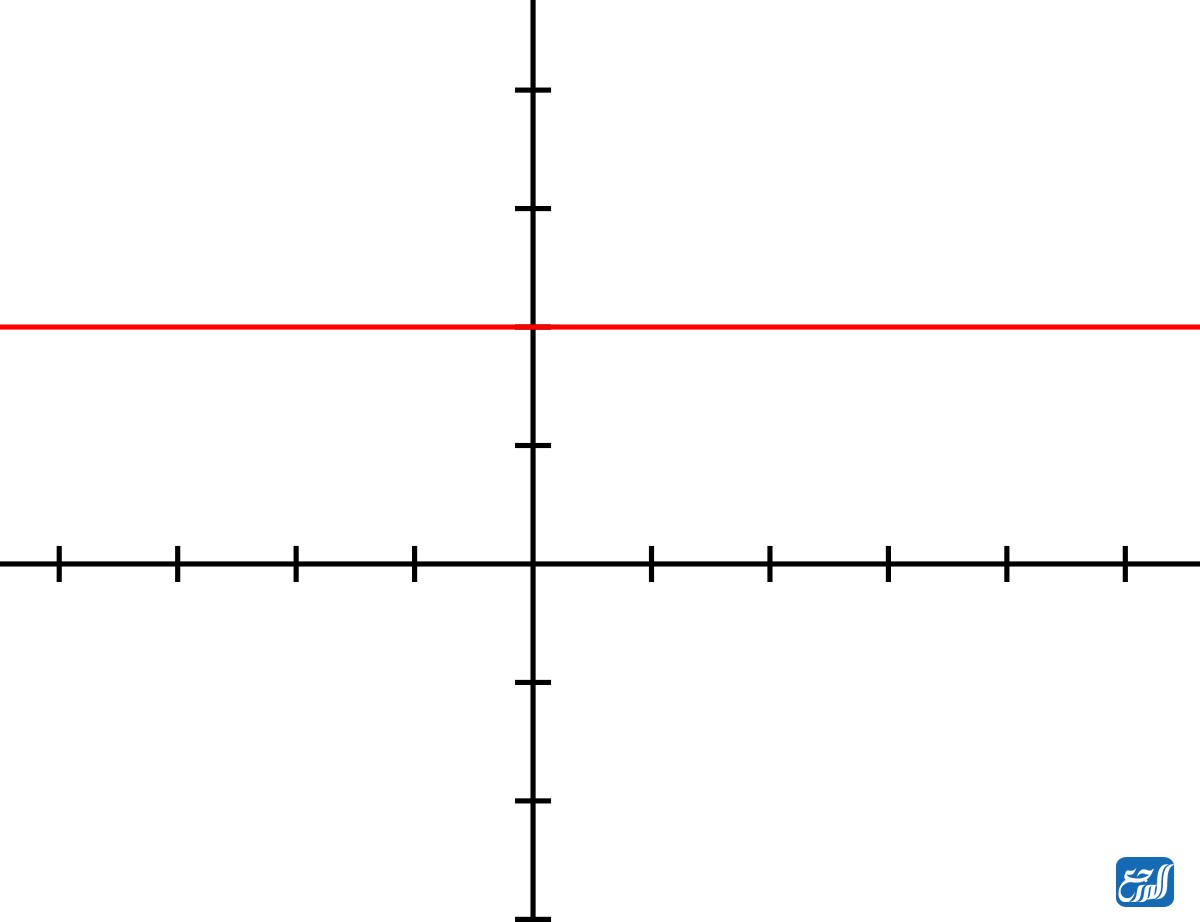
تعد الدالة الثابتة نوع من أنواع الاقترانات كثيرة الحدود، وتكون فيها درجة الاقتران كثير الحدود صفر، أي أن الأس الموجود على المتغير (س) فيها يساوي صفر، وبالتالي تكون هذه الدالة عبارة عن ثابت (عدد معين). وصيغة الدالة الثابتة هي: (f (x) =a)وفيما يأتي التمثيل البياني للاقتران الثابت.

الدالة الخطية الأم

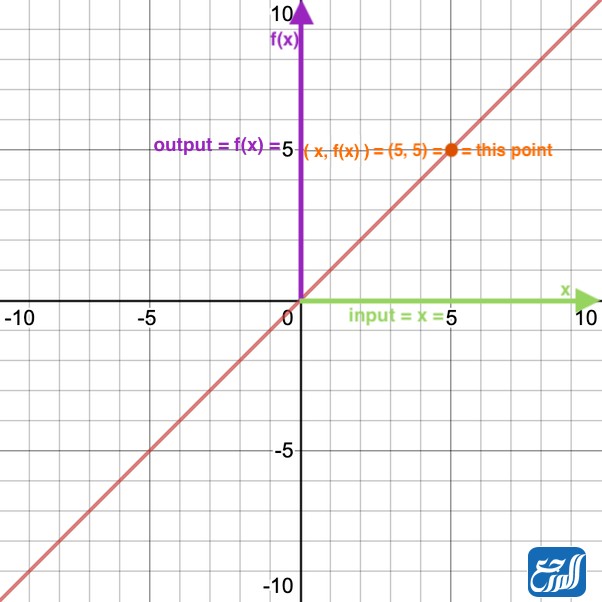
الدالة الخطية هي من دوال كثيرات الحدود من الدرجة الأولى، وفيها يكون المتغير مرفوع للقوة واحد، وصيغتها العامة هي: (f (x) =ax +c)، وترسم الدالة الخطية من خلال الاعتماد على نقطتين من المجال وإيجاد صورتهما ومن ثم التوصيل بينهما بخط، وللحصول على نتيجة دقيقة يمكن أخذ 5 نقاط. [1]

والدالة الخطية الأم هي: (f (x) =x)

الدالة التربيعية الأم

الدالة التربيعية هي واحدة من أنواع كثيرات الحدود، ودرجة الاقتران هي الثانية، أي أن الأس الأكبر فيها هو 2، وصورتها القياسية هي (f(x) = ax² +bx + c) ويقطع الاقتران التربيعي السينات مرتان، ويتم رسم التمثيل البياني له عن طريق إيجاد صور لثلاث نقاط؛ والتي هي أصفار الاقتران وقمة المنحنى أو ما يعرف بصورة رأس القطع التي ينقسم منحنى الاقتران إلى جزأين متماثلين.

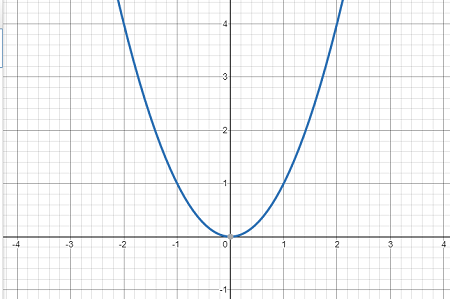
الدالة التربيعية الأم : f(x) = x² ، والرسم الآتي يمثل التمثيل البياني للدالة التربيعية الأم.

دالة الجذر التربيعي الأم

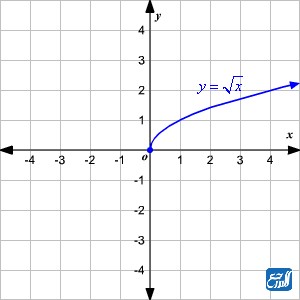
الدالة الجذرية هي نوع من أنواع الدوال الحقيقية، تكتب بالصيغة  القياسية الآتية: f(x) = √g(x). حيث يكون هـ اقتران كثير الحدود. ومن أجل رسم هذه الدالة يجب علينا أولًا تحديد مجال الاقتران ثم إيجاد صور لمجموعة عناصر من المجال ومن ثم إسقاط النقاط الناتجة ورسم التمثيل البياني لها في المستوى الديكارتي. ومجال الاقتران الجذري هو جميع القيم التي تجعل ما تحت الجذر أكبر من أو يساوي صفر. [2]

دالة الجذر التربيعي الأم: f(x) = √x ، والرسم البياني الآتي بين دالة الجذر التربيعي الأم:

الدالة النسبية الأم

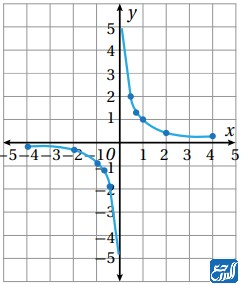
الاقترانات النسبية هي نوع من أنواع الدوال، وهي الدوال التي يمكن كتابتها بصورة كسر (بسط ومقام) بين كثيري حدود، والصيغة القياسية له هي: (f (x) /g (x)، حيث إن g (x) لا يجوز أن يكون مساويًا للصفر. ويمكن تحديد مجال الاقتران النسبي من خلال تحديد أصفار المقام، فالمجال هو مجموعة الأعداد الحقيقية عدا ما يجعل المقام مساويًا للصفر. وحساب مجال الاقتران النسبي يكون من خلال تحليل كثير الحدود في المقام وإيجاد الأصفار واستثنائها من مجموعة الأعداد الحقيقية.

الدالة النسبية الأم: f(x) = 1/x، وتسمى أيضًا بالاقتران المقلوب، ويكون جزأي الاقتران متماثلات بالنسبة لنقطة الأصل. والصورة الآتية تمثل الدالة النسبية الأم:

شاهد أيضًا: بحث عن الطرائق العلمية في الكيمياء

الدالة الدرجية الأم

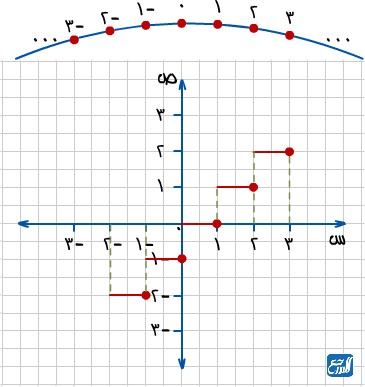
اقتران أكبر عدد صحيح الذي يعرف الدالة الدرجية بسبب شكله المشابه للدرج يعد من أنواع الدوال الحقيقية، وهو اقتران يقرن فيه كل عدد حقيقي صحيح أقل من أو يساوي المتغير x، ويرمز لأكبر عدد صحيح بالرمز [x]. وإذا كان n≤x<n+1 ، حيث إن n عدد صحيح، فإن f(x) = [x] = n.

الدالة الدرجية الأم: f(x) = [x]. والصورة الآتية تمثل الدالة الدرجية الأم:

دالة القيمة المطلقة الأم

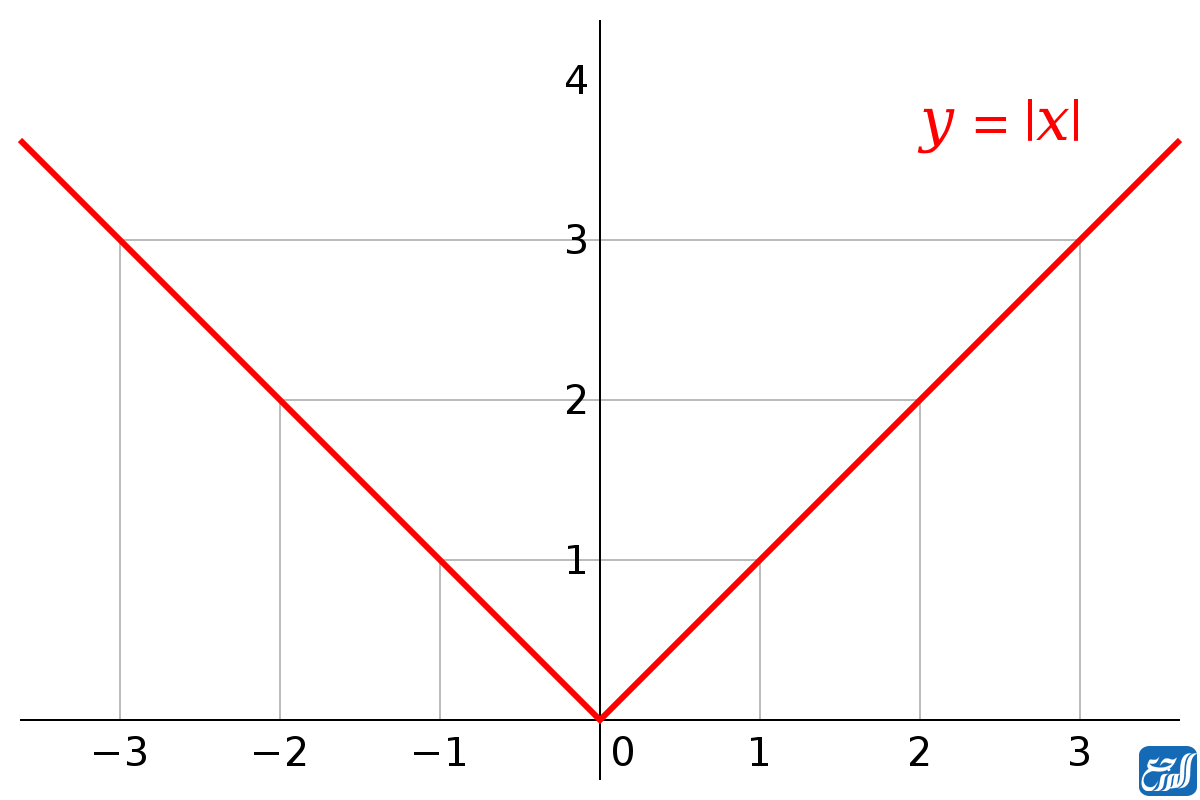
القيمة المطلقة تعني بعد النقطة عن الصفر على خط الأعداد، أي أن العدد الناتج عنها يكون من غير إشارة، والصيغة العامة له هي f(x) = ιg(x)ι، وهذا يعني أن جميع إجابات اقتران القيمة المطلقة سوف تكون موجبة وكذلك الرسم البياني له لن ينزل إلى الحيز السالب في حال يم يضاف له شيء خارج نطاق القيمة المطلقة، ومنحناها يأخذ شكل الحرف V، ولرسمها يجب إعادة تعريفها من خلال معرفة إيجاد المجال بحيث تكون نقطة التشعب هي النقطة التي يتفرع منها خطي المنحنى.

دالة القيمة المطلقة الأم: f(x) = ιxι، والصورة الآتية تمثل الدالة الدرجية الأم:

خصائص الدالة الرئيسية الأم

يمكن أن نجد لكل واحدة من الدوال الأم التي ذكرناها سابقًا الخصائص التي تميزها عن غيرها، من حيث ذكر المجال، والمقطع السيني والصادي، وفيما إذا كان المنحنى له نصفان متماثلان، وإن كان متصلًا أو غير متصل، وما هي بداية المنحنى ونهايته، أي نقطة البداية والنهاية لمداه، ووصف الدالة من حيث التزايد والتناقص. وفيما يأتي سوف نضع لكم مثلًا على خصائص الاقتران التربيعي: f(x) = x²:

• مجال الدالة هو مجموعة الأعداد الحقيقية (ح)، ومداه هو [0، ∞).
• ليس للمنحنى سوى مقطع سيني وصادي واحد وهو يمثل أيضًا رأس القطع، وهي النقطة (0،0).
• المنحنى متماثل من محور التماثل التي تمر من النقطة (0،0).
• الدالة زوجية.
• المنحنى متصل عند جميع قيم المجال.
• يبدأ المنحنى عند x=0 ، وتكون (∞ = _∞→lim_{x ⁾}، أي نهاية الاقتران عندما x تؤول إلى المالانهاية هي المالانهاية.

شاهد أيضًا: بحث عن الرياضيات كامل

تعريف التحويلات الهندسية على الدوال الأم

التحويلات الهندسية على الدوال الأم هي مجموعة من العمليات التي يتم إجراؤها على الدوال الأم فتؤثر فيها مما يغير في شكل منحنى الدالة الأم، من حيث الموقع ومن حيث الشكل والأبعاد، وهي نوعان: [3]

• التحويلات الهندسية القياسية: وهي التي تغير موقع المنحنى فقط، ولا تغير شكله أو أبعاده.
• التحويلات غير الهندسية القياسية: وهي التي تغير شكل المنحنى أو أبعاده.

أنواع التحويلات الهندسية على الدوال

كما ذكرنا فإن التحولات القياسية هي التغيرات التي تطرأ على الدالة الأم مما يؤدي إلى تغير شكلها وأبعادها وموقعها، وذكرنا أن ما يغير موقعها فقط تسمى التحويلات القياسية أما التي تغير الشكل والأبعاد في ما يسمى التحويلات غير القياسية. ومن أمثلة التحويلات القياسية الانسحاب (الإزاحة)، والانعكاس، ومن أمثلة التحويلات غير القياسية التمدد والتحويلات التي تطرأ من وضع القيمة المطلقة. وسوف نتناول أنواع التحويلات الهندسية على الدوال الأم بالتفصيل: [4]

انسحاب الدوال الرئيسية الأم

يٌعد الانسحاب من التحويلات الهندسية القياسية، وهو من التغيرات التي تعمل على نقل موقع المنحنى، وتقسم إلى قسمين؛ الانسحاب الرأسي للدوال وهو يتعلق بنقل منحنى الدالة إلى الأعلى وإلى الأسفل، والانسحاب الأفقي وهو الذي ينقل منحنى الدالة إلى اليمين وإلى اليسار. [5]

الانسحاب الرأسي للدوال

الانسحاب الرأسي هو التي يكون عندها منحنى الدالة منزاحًا إلى الأعلى أو إلى الأسفل نتيجة زيادة رقم موجب أو سالب إلى الاقتران، وصورته: (g(x) = f(x) +k )، بحيث عندما تكون قيمة k أقل من صفر ينزاح المنحنى إلى الأسفل بعدد k من الوحدات، أما عندما يكون k أكبر من صفر ينزاح المنحنى إلى الأعلى بعدد k من الوحدات. كما في الشكل الآتي:

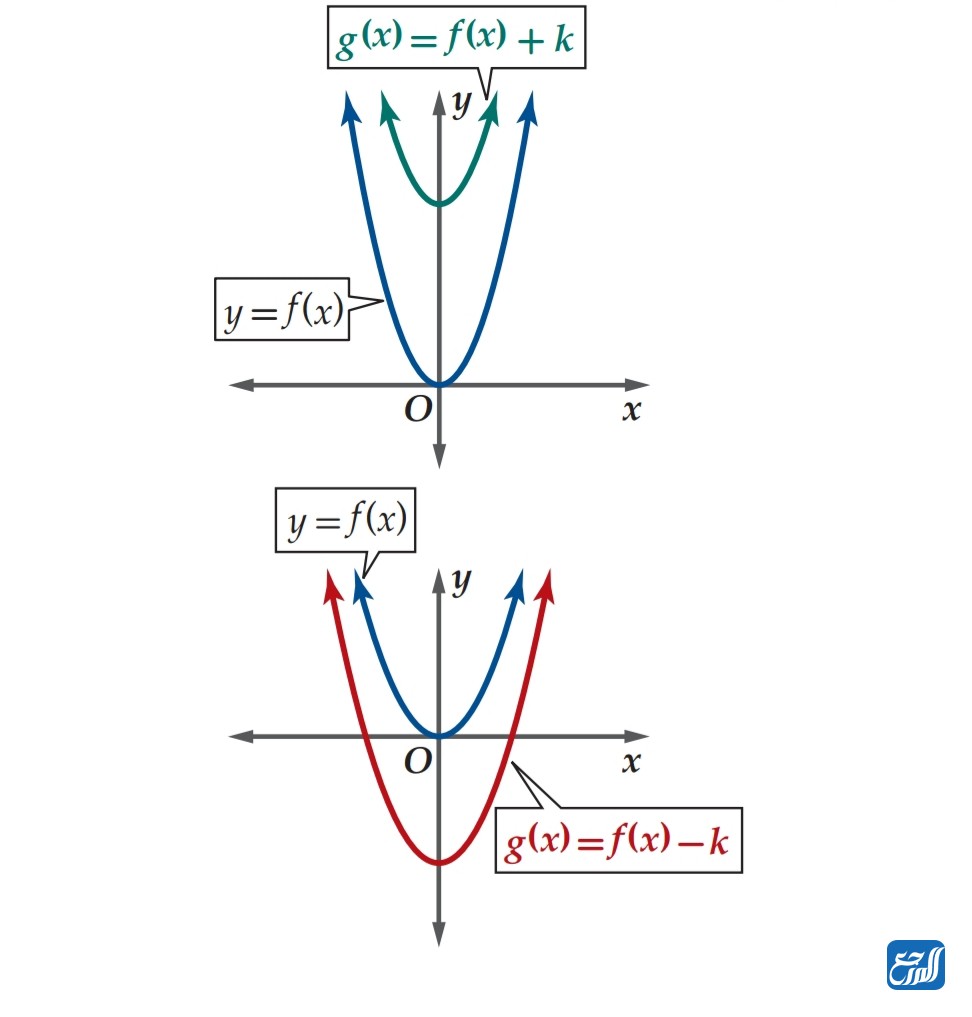
الانسحاب الافقي للدوال

الانسحاب الأفقي هو التي يكون عندها منحنى الدالة منزاحًا إلى اليمين أو إلى اليسار نتيجة زيادة رقم موجب أو سالب إلى المتغير، وصورته: (g(x) = f(x-h)  )، بحيث أن قيمة h عندما تكون أقل من صفر فإن المنحنى سوف ينزاح المنحنى إلى اليسار بعدد h من الوحدات، أما عندما تكون قيمة h أكبر من صفر سوف ينزاح المنحنى إلى جهة اليمين بعدد h من الوحدات. كما في الشكل الآتي:

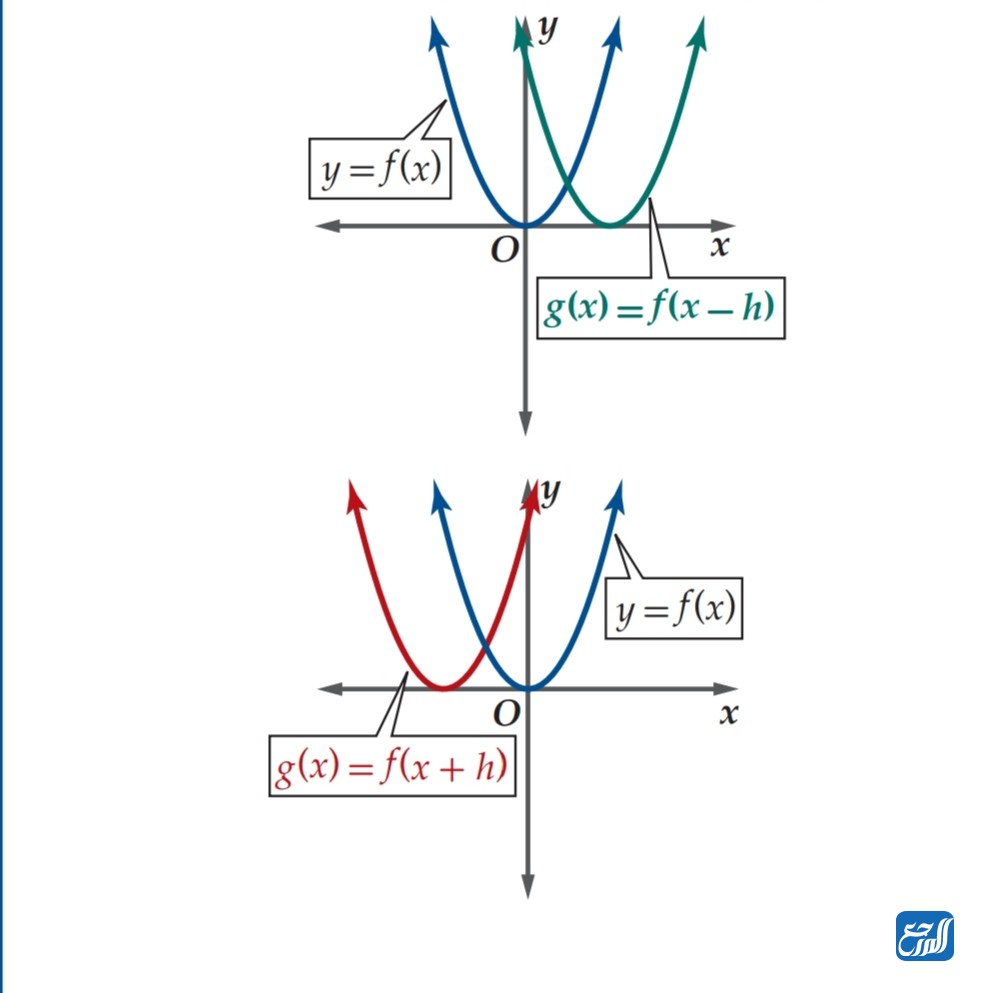
شاهد أيضًا: بحث عن الفطريات وطرق تكاثرها

الانعكاس حول المحورين الاحداثيين للدوال الرئيسية الأم

يعد الانعكاس من التحويلات الهندسية القياسية، ويكون فيها لمنحنى الدالة صورة عكسية كالمرآة بالنسبة إلى مستقيم محدد، وتنقسم إلى قسمين؛ هما الانعكاس حول محور السينات، والانعكاس حول محور الصادات، وسوف نبين هذان النوعين فيما يأتي:

الانعكاس حول المحور السيني

منحنى الدالة  g(x) = – f(x) يمثل انعكاسًا للدالة f(x) حول محور السينات (x). ويمثل الرسم الآتي توضيحًا لهذا النوع من الانعكاس:

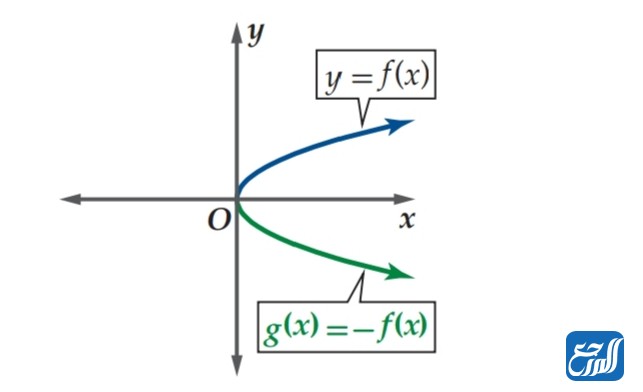
الانعكاس حول المحور الصادي

منحنى الدالة  g(x) = f(-x) يمثل انعكاسًا لمنحنى الدالة f(x) حول محور الصادات (y). ويمثل الرسم الآتي توضيحًا لهذا النوع من الانعكاس:

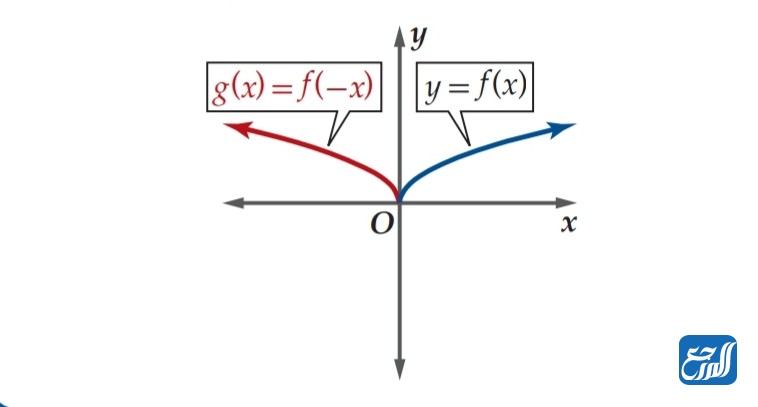
تمدد الدوال الرئيسية الأم

يعدد التمدد نوع من أنواع التحويلات الهندسية غير القياسية للدوال الرئيسية الأم، وهو يؤدي إلى تضييق أو توسيع منحنى الدالة بشكل رأسي أو أفقي، وينقسم إلى نوعين التمدد الأسي، والآخر هو التمدد الأفقي، وسوف نبين لكم فيما يأتي هذين النوعين:

التمدد الرأسي للدوال

إذا كان الرقم a يمثل عددًا حقيقيًا موجبًا، فإن منحنى الدالة g(x) = af(x)  هو عبارة عن توسع رأسي ومط لمنحنى f(x) إذا كان الثابت a له قيمة أكبر من واحد، أما إذا كانت قيمة الثابت أقل من واحد وأكبر من صفر أي بينهما فإن المنحنى g(x) سوف يمثل تضييق رأسي أي ضغط لمنحنى الدالة f(x).

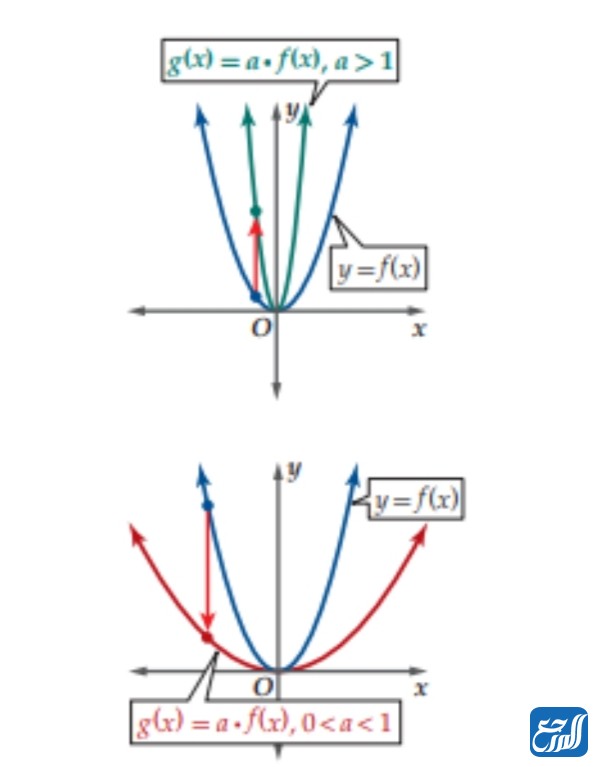
التمدد الأفقي للدوال

في حال أن الرقم a كان عددًا حقيقيًا موجبًا، فإن منحنى الاقتران g(x) = f(ax)  سوف يكون تضيق أفقي وضغط لمنحنى f(x) إن كان الثابت له قيمة تساوي رقمًا أكبر من 1، أما في حال كانت قيمة الثابت a بين الرقمين واحد وصفر؛ أي أقل من واحد وأكبر من صفر فإن المنحنى g(x)  سوف يمثل توسع أفقي ومط لمنحنى الاقتران f(x).

 

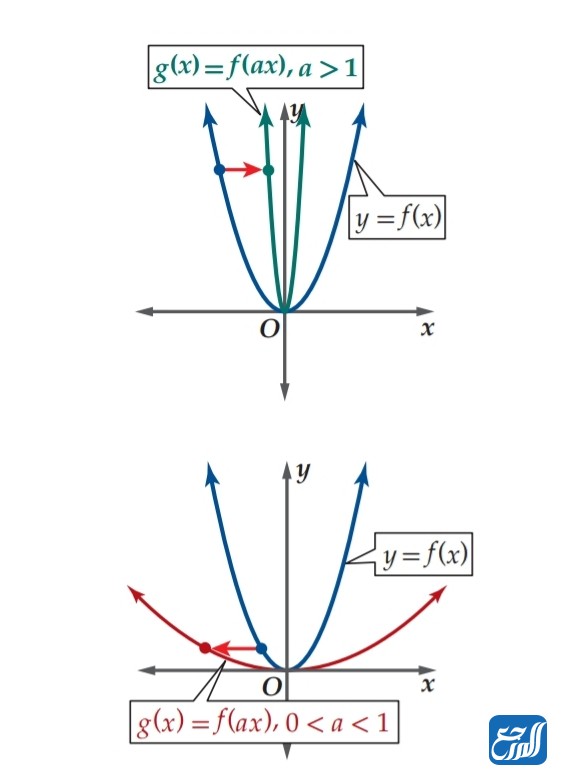
التحويلات الهندسية مع دوال القيمة المطلقة

تعد تحويلات القيمة المطلقة من التحويلات الهندسية التي يتم إجراؤها على بعض الدوال وهي من التحويلات غير القياسية، وتنقسم إلى نوعين كما يأتي:

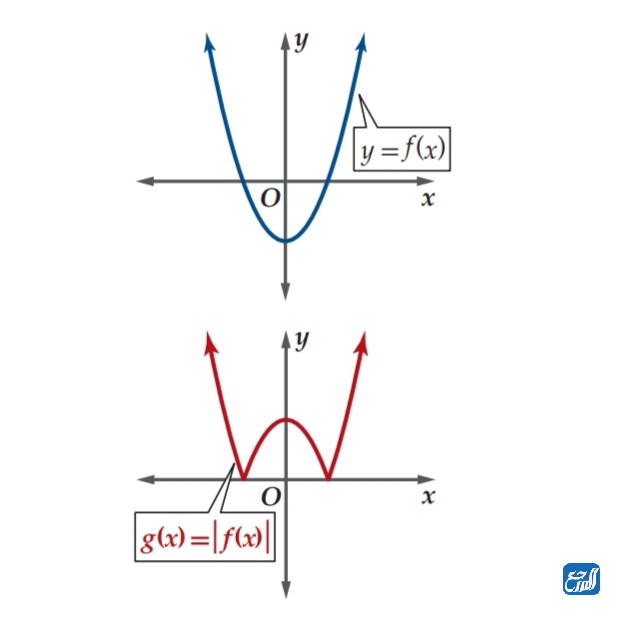
• g(x) = ιf(x)ι : يغير هذا النوع من التحويل الجزء الذي يقع تحت محور السينات الموجب من منحنى الاقتران حتى ينعكس ويصبح فوق المنحنى، فيكون انعكاسا لهذا الجزء حول محور السينات الموجب. وهي الصورة الأولى في الأسفل.
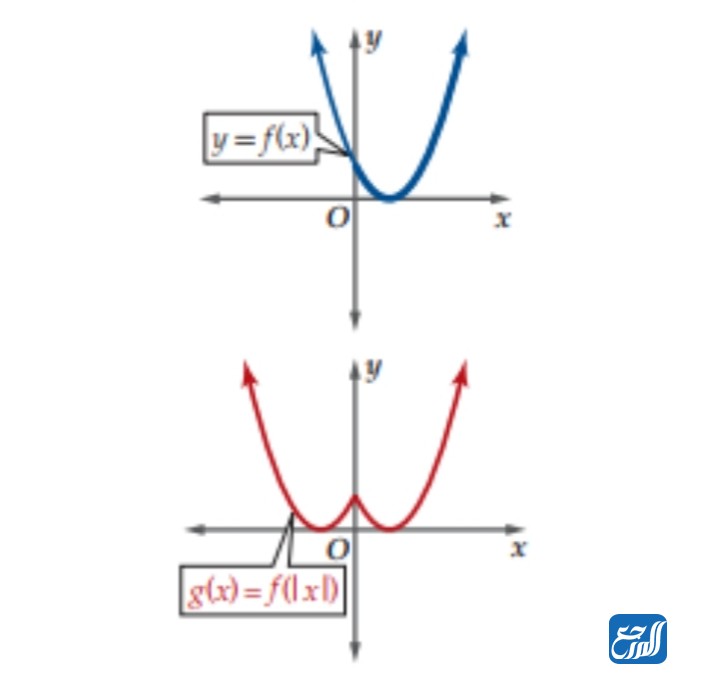
• g(x) =f(ιxι) : هذا النوع من التحويلات الهندسية يطرأ على جزء من الاقتران الذي يقع إلى يسار منحنى الصادات، فيصبح مكانه صورة للجزء الذي يقع على يمين محور الصادات من المنحنى، فيكون عبارة عن انعكاس حول محور الصادات للجزء الواقع على اليمين. وتمثل الصورة الثانية في الأسفل.

شاهد أيضًا: بحث عن الكيمياء الكهربائية كامل

خاتمة بحث عن الدوال الرئيسة الام والتحويلات الهندسية

وخي ختام موضوع البحث عن الدوال الرئيسة الأم والتحويلات الهندسية لا بد من التأكيد على أهمية دراسة هذا الموضوع لما له من تطبيقات كبيرة يمكن الاستفادة منها خلال الأعمال المختلفة من خلال استحداث البرامج والتمثيلات البيانية التي تعتمد بشكل خاص على التحويلات الهندسية التي تطرأ على الدوال الأم.

فمن الصور الحياتية للاستفادة من التحويلات الهندسية في الحياة العامة دراسة الفرق بين سعر الإنتاج والتكاليف بعد خفضها أو رفعها من خلال إجراء تعديلات على دالة الإنتاج الأساسية ثم دراسة المنحنيين قبل وبعد من أجل فهم التأثير. بالإضافة إلى وجود الكثير من التطبيقات الأخرى التي يمكن الاستفادة منها.

بحث عن الدوال الرئيسة الام والتحويلات الهندسية pdf

الدوال هي عبارة عن علاقة بين المتغيرات والأرقام وما يميزها عن العلاقات أن عل عنصر في المجال يرتبط بعنصر واحد في المدى، ويستفاد من دراسة الدوال في الكثير من العلوم والتطبيقات في الحياة، فالدوال ترتبط ارتباطًا رئيسيًا بدراسة النهايات والاتصال، وبدراسة الاشتقاقات وتطبيقات التفاضل، فضلًا عن أهميتها في دراسة علوم التكامل وتطبيقاتها، بالإضافة إلى أهميتها في الكثير من العلوم الفيزيائية والكيميائية وحتى الحياتية والإنسانية. ويمكنكم “من هنا” تحميل بحث عن الدوال الرئيسة الام والتحويلات الهندسية pdf.

بحث عن الدوال الرئيسة الام والتحويلات الهندسية واضح doc

كتابة بحث عن الدوال الرئيسة الام والتحويلات الهندسية من الأمور المهمة جدًا من أجل فهم الدوال والتحويلات الهندسية التي تطرأ عليها، والتطبيقات ذات العلاقة بهذا النوع من العلوم. ويعد برنامج الوورد البرنامج الأفضل لكتابة الأبحاث بالنسبة إلى الطلاب وذلك يعود إلى ما يتيحه هذا البرنامج من إمكانية للكتابة والتعديل، بالإضافة إلى سهولة كتابة المعادلات من خلال صور المعادلات الجاهزة والمدرجة في البرنامج، فضلًا عن إمكانية إدراج الصور بسهولة أيضًا. ويمكنكم تحميل بحث جاهز عن الدوال الرئيسة الأم والتحويلات الهندسية واضح “من هنا” بصيغة doc.

وفي ختام هذا المقال، نكون قد أدرجنا لكم بحث عن الدوال الرئيسة الام والتحويلات الهندسية واضح بالصيغتين doc و pdf، يتضمن مجموعة من المعلومات الرياضية المدعمة بالصور عن الدوال الرئيسية الأم وتأثير التحويلات الهندسية عليها.