بحث عن المنصفات في المثلث

ِبحث عن المنصفات في المثلث، في علمِ الريّاضياتِ تتنوعُ الأشكالَ الهندسيّة ما بينَ المُثلث والمُربع والدائِرّة وشبه المُنحرف ومتوازي الأضلاع وغيّرها من الأشكالِ الأُخرى، ويتميّزُ كل شكل هندسي بخواصٍ مُختلفة ومُغايّرة عن الأشكالِ الأخرى، كما أنّه يتبعُ لقوانين مُعينّة، ومن خلالِ موقع المرجع سنُخصص الحديثَ عن المُثلث وخواصّه والمُنصفات في المُثلث.

مقدمة بحث عن المنصفات في المثلث

المُثلث هو أحدُ الأشكال الهندسيّة المُغلقة، يُصنفُ على أنّه ثلاثيّ الأضلاع والزوايّا، حيثُ أنّه يتكوّن من ثلاث قطع مستقيمة تُشكّل الأضلاع، وتتقاطع في نهايتها لتكوين الرؤوس أو الزوايا، ويتمتعُ المثلثُ بمجموعةِ من الخصائص المُختلفة، كأن يكونُ مجموع قياساتِ زوايّاهُ يساوي 180 درجّة، وأن الضلع الأطول في المثلثِ يُقابل الزاويّة الأكبر، وغيّرهُ، وللمثلثُ أنواع عدّة حسبْ أطوال أضلاعِه وقياساتِ زوايّاه، وفي بحثنا سنركزُ الحديثَ بشكل مُفصل عن المنصفاتِ في المثلثْ والذي يوجدُّ لهُ عدّة أنواع مثلَ العمودُ المنصفِ، ومركزُ الدائرة الخارجيّة للمثلث، ومُنصف الزاويّة، ومركز الدائرة الخارجية للمثلثِ.

شاهد أيضًا: مركز المثلث هو نقطة تلاقي

بحث عن المنصفات في المثلث

في بدايةِ بحثنا لا بدّ من التطرقِ إلى تعريفِ المُثلث وخواصّه وكيفيةِ إيجاد مسّاحته ومُحيطه وارتفاعّه، وماهيّةُ المنصفات على نحوِ الوتيّرة الآتيّة:

تعريف المثلث

يُمكن تعريف المثلث (بالإنجليزية: Triangle) على أنّه مُضّلع مُغلق، ثنائي الأبعاد، وثلاثي الأضلاع، حيثُ أنّ لهُ ثلاثةُ أضلاع، وثلاث رؤوس، وثلاث زوايا مجموعُ قيّاسِها يُساوي 180 درّجة، ودومًا ما يُقابل أطول طول في المثلث أكبرُ زاويّة داخليّة، أما أقصرُ ضلعَ في المُثلث فيُقابله أصغرُ زاويّة داخليّة، وتتمُّ تسميةُ المثلث غالبًا بالاعتمادِ على رؤوسِه.[1]

خصائص المثلث

يتمتعُ المثلث بمجموعة من الخصائص، ويُمكنُ تلخيصُ خصائصِ المثلث في النقاطِ الآتيّة:[2]

• مجموع زوايّا المُثلث يُساوي 180 درجة.
• الضلع الأطول في المثلث هو الضلعُ الذي يقابلُ الزاويّة الأكبرُ في المثلث.
• مجموع طولُ أي ضلعين من أضلاع المُثلث أكبر من طول الضلع الثالث.
• الفرقُ بين أي ضلعين من أضلاع المثلث أقصرُ من طول الضلع الثالث.
• إذا وازى مستقيم أحد أضلاع المثلث وقطع الضلعين الآخرين فإنّه يقسم المثلث إلى مثلثات متشابهة ومتناسبة في الطول.
• الزاوية الخارجيّة للمثلث تساوي مجموع الزوايا الداخليّة المقابلة لها أو البعيدة عنها، ويكون مجموع الزوايا الخارجيّة للمثلث هو 360 درجة.
• يُعرف المثلث الذي تكونُ قياسات زوايّاه أقل من 90 درجة بالمثلث حاد الزاويّة، فيما يُعرف المثلث الذي تكونُ قياسات زواياه أكبر من 90 درجة بالمثلث منفرج الزاوية.
• يقسم الارتفاع المثلث متساوي الساقين والمثلث متساوي الأضلاع القاعدة إلى نصفين متساويين، كما يقسم المثلث إلى مثلثين متساويين.
• يتشابه المثلثان إذا كانت الزوايا المتقابلة لكل من المثلثين مُتطابقة وأطوال أضلاعهما مُتناسبة.

أنواع المثلثات

يمكنُ تصنيف المُثلثات بناءً على قياسِ الزوايّا وأطوال الأضلاع على النحوِ الآتّي:

أنواع المثلثات حسب طول الأضلاع

تصنفُ المثلثات حسبْ طول الأضلاع إلى الآتّي:

• المثلث متساوي الأضلاع: في المثلث متساوي الأضلاع تتساوى أطوال الأضلاع، وتتساوى قياسات الزوايّا بحيثُ يكونُ قياس كُلُ زاويّة يُساوي 60 درجة.
• المثلث متساوي الساقين: في المثلث متساوي الساقين يتساوى ضلعين فقط في الطول، وتتساوى زاويتينِ فيّه، وهُما زوايتي قاعدةِ المثلث.
• المثلث مختلف الأضلاع: في المثلث مُختلف الأضلاع لا تتساوى أطوال الأضلاع، ولا تتساوى قياسات الزوايا.

أنواع المثلثات حسب الزوايا

تُصنفُ المثلثات حسب قياسات الزوايا إلى الآتي:

• المثلث حاد الزوايّا: هو المثلث الذي تكونُ قيّاس كُل زاويّة من زواياه أقلُّ من 90 درجة.
• المثلث منفرج الزوايّة: هو المثلث الذي تكونُ بّه زاويّة قياسّها أكبرُ من 90 درجة.
• المثلث قائم الزاويّة: هو المثلث الذي تكونُ بّه زاوية قائمة قياسها 90 درجة.

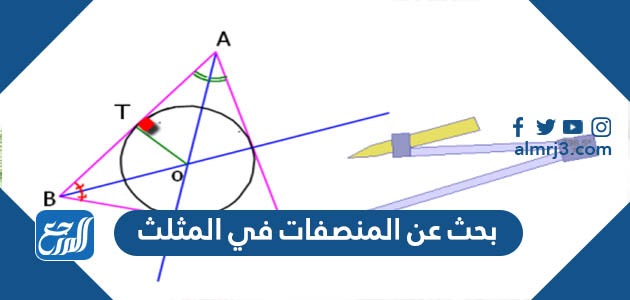
المنصفات في المثلث

المُنصف هو مُستقيم يرسمُ بداخلِ المثلث، ويوجدُّ له عدّة أنواع ومنّها:

العمودُ المنصف

يُعرفُ العمود المُنصف على أنّه مستقيم يقطعُ قطعة مُستقيمّة عند منتصفها ويكونُ عموديًا على تلكَ القطعّة، ويتبعُ العمود المُنصف لنظرتينِ وهُما:

• نظريةُ العمود المنصف:

تنصُّ نظرية العمود المُنصف على أن كُلُ نقطة على العمود المنصف لقطعة مُستقيّمة تكونُ على بُعدين مُتساويين من القطعة المُستقيّمة.

• عكسُ النظريّة:

وتُسمى عكسُ نظريّة العمود المُنصف وتنصُّ على أن كُلُ نقطة على بعدين مُتساويين من طرفي قطعة مُستقيّمة، فإنّها تقعُ على العمود المُنصف لتلكَ القطعّة.

مركز الدائرة الخارجية للمثلث

تنصُّ نظرية مركز الدائرة الخارجية للمثلث على أنّ الأعمدة المُنصفة للمثلث تلتقي في نقطة تُسمى مركزُ الدائرة الخارجيّة للمُثلث، وتكون هذه النقطة على أبعاد مُتساويّة من المثلث.

مُنصف الزاوية

يُعرفُ منصف الزاويّة على أنّه نصف مُستقيم يقسمُ الزاويّة إلى زاويتينِ مُتطابقتين، وقد سُميّ نصفُ مستقيم لأنّ لهُ بدايّة لكنّه ليس لهُ أيُّ نهاية، ويتبعُ منصف الزاويّة إلى نظريّة وهِيّ:

• نظريةّ منصف الزاوية: 

تنصُ نظرية منصف الزاوية على أنّه كُلُ نقطة تقعُ على منصف الزاوية تكونُ على بُعديّن مُتساويينِ من ضلعيهما.

مركز الدائرة الداخلية للمثلث

تنصُّ نظرية مركز الدائرة الداخلية للمثلث على أنّ منصفات زوايا أيُّ مثلث تتقاطعُ عندَ نقطة تُسمى مركز الدائرة الداخليّة للمُثلث، وهِي على أبعاد مُتساويّة من أضلاعِه.

متوسط المثلث

يُعرّف متوسط المُثلث بأنّه قطعة مُستقيمّة تصلُّ من إحدى زوايّا المُثلث إلى مُنتصفَ الضلع الذي يُقابّله، ولهذا الخطُّ المتوسط خصائصٌ عدّة، ومنّها:

• لكل مثلث ثلاثة متوسطات، متوسط لكل رأس وضلع مقابل له.
• كُل خط متوسط يُنصفُ المثلث إلى مُثلثينِ مُتساويين في المساحة، لأن لهما قاعدتين متساويتين، ولهما نفس الارتفاع.
• في المثلث متساوي الساقين والمثلث متساوي الأضلاع ينصفُ الخط المتوسط زاوية الرأس المحصورة بين ضلعين متساويين إلى زاويتين متساويتين.
• تتقاطع خطوط المتوسط في المثلث في نقطة تُسمّى بالنقطة المركزيّة، تقسم كل خطّ متوسط من الخطوط المتوسطة الثلاث بنسبة 2:1.
• يُمكن إيجاد طول الخط المتوسط عن طريق نظرية أبولونيوس:
  • م _أ=((2بَ²+2جَ²-أَ²)÷4)√، أو م _ب=((2أَ²+2جَ²-بَ²)÷4)√، أو م _ج=((2بَ²+2أَ²-جَ²)÷4)√؛ حيث:
  • م _أ: طول خط المتوسط النازل من الرأس أ، أَ: طول الضلع المقابل للرأس أ.
  • م _ب: طول خط المتوسط النازل من الرأس ب، بَ: طول الضلع المقابل للرأس ب.
  • م _ج: طول خط المتوسط النازل من الرأس ج، جَ: طول الضلع المقابل للرأس ج.

خاتمة بحث عن المنصفات في المثلث

المُنصفات في المثلث هِي المُستقيّمات التي تُنصفُ أضلاع المُثلث أو تنصفُ زوايّا المثلث، ويوجدُ للمنصفاتِ عدّة أنواع ومنّها العمودُ المنصف وهوَ المُستقيّم الذي ينصفُّ القطعةُ المستقيمة في مُنتصفِها ويتعامدُ عليّها، ويتبعُ العمودُ المُنصف لنظرتينِ مُتعاكستين، أما النوعُ الثانّي من المُنصفات هوَ مركزُ الدائرة الخارجيّة للمُثلث والذي يوضحُ كيفية التقاءَ الأعمدة المنصفة في منطقة مركز الدائرة الخارجيّة، والنوعُ الثالث هو منصفُ الزاويّة والتي هوَ عبارة عن نصف مُستقيم له بداية وليس لهُ نهايّة ويقسمُ الزاويّة إلى زاويتينِ مُتطابقتين، أما النوعُ الرابع هوَ مركزُ الدائرة الداخليّة للمثلث حيثُ أنّ منصفات زوايا المثلث تتقاطع عند نقطة المركز للدائرة الداخليّة للمثلث.

بحث عن المنصفات في المثلث pdf

ما يُميّزُ بحوثِ pdf أنّه يمكنُ طباعتّها بسهولّة وبدقّة فائقة، والمثلثُ هوَ شكلٌ هندسيْ لهُ ثلاثُ أضلاع، وثلاثُ زوايّا، وثلاثُ رؤوس، ومن أهم المُصطلحاتِ التي تتعلقُ بالمثلثِ مصطلحُ الرأس وهوَ زاويّة المثلثِ، ومصطلحُ القاعدة حيثُ يمكن أن يشكّل أي ضلع من أضلاع المثلثِ قاعدة له، لكنها عادةً ما تكون الضلع المرسوم في الأسفل، وفي بحثِنا عن المنصفاتُ في المثلثِ تحدثنا بشكل واضح عن مصطلح المنصفات وأنواعِها، ويمكن تحميل بحثْ عن المنصفاتِ في المثلثِ بصيغةِ pdf “من هنا“.

شاهد أيضًا: شرح درس المنصفات في المثلث

بحث عن المنصفات في المثلث doc

قد يرغبُ بعضَ الأشخاص بقراءةِ بحوثهمِ بصيغةِ ملف الوورد، حيثُ تكن الرؤية أوضحَ، والخُطوطُ أدّق، والعبارات مُنسقّة ومُرتبّة بشكل مَرن، كما يمكنّهم من التعديلِ عليّه بأيّ وقت يرغبون، أو إضافةِ معلوماتٍ هامة أو تحديدها بلونٍ مُغايّر للرجوعِ إليّها وقتُ الحاجة، وفي بحثِنا عن المنصفاتِ في المثلثِ فإننّا أدرجنا كُلُ ما يتعلقُ بالمنصفاتِ بشكل واضح وسلس فضلاً عن التعريف الريّاضي للمُثلث وخواصه، وخواصُ متوسط المُثلث أيضًا، ويمكن تحميل بحثْ عن المنصفاتْ في المثلثِ بصيغةِ doc “من هنا“.

إلى هُنا نكونُ قد وصلنا إلى نهايةِ مقالنا بحث عن المنصفات في المثلث، حيثُ سلطنا الضوء على مفهومِ المُنصفات في المُثلث والنظريّات التي يتبّعُ لها.