بحث عن المصفوفات في الرياضيات كامل

بحث عن المصفوفات في الرياضيات كامل من الأبحاث المهمة جدًا والتي ينبغي تسليط الضوء عليها من خلال عمل العروض التقديمية للطلاب وتكليفهم بإعداد الأبحاث عنها والبحث عن أهم التطبيقات التي تعتمد بشكل أساسي على المصفوفات، فعلى الرغم من افتقار معظم المناهج المدرسية إلى تدريس المصفوفات بالشكل الوافي الذي يتناول تطبيقاتها وأهميتها إلا أن من المهم أن نعطيها حقها، لهذا فإن موقع المرجع سوف يدرج لكم بحث عن المصفوفات يتناول فيه الحديث عن المصفوفات من جوانبها المختلفة.

مقدمة بحث عن المصفوفات في الرياضيات

بسم الله الرحمن الرحيم، والحمد لله رب العالمين، والصلاة والسلام على سيدنا وهادينا محمد سيد الخلق والمرسلين وعلى آله وأصحابه أجمعين، أما بعد:

البحث الذي أنا في صدد الكتابة عنه هو بحث مهم عن واحد من أهم علوم الرياضيات وهو المصفوفات؛ حيث إن المصفوفة لها تاريخ طويل العديد من التطبيقات التي منها حل المعادلات الخطية، وقد كانت تُعرف باسم المصفوفات (arrays) حتى القرن التاسع عشر ومن ثم أطلق عليها (matrix) وهذا هو الاسم المعتمد إلى يومنا هذا. ويمكن استخدام المصفوفات للتعامل مع نظام مكون من معادلات خطية متعددة في وقت واحد وحلها من خلال إيجاد قيم المتغيرات، كما تكشف المصفوفات وعملية ضرب المصفوفات عن ميزاتها الأساسية عند ارتباطها بالتحولات الخطية (linear transformations)، والتي تعرف أيضًا باسم الخرائط الخطية (linear maps).

شاهد أيضًا: بحث عن الخوارزمي كامل

بحث عن المصفوفات في الرياضيات كامل

نظرًا لأهمية البحث في المصفوفات ودراستها دراسة وافية لما يتعلق بها من التعريف بمفهومها العام وذكر أهم تطبيقاتها في الحياة اليومية، وأهم العمليات التي تجري عليها والكثير من الأمور الأخرى، فإنني في هذا البحث سوف أسلط الضوء على كل هذه الموضوعات بالتدريج من خلال تصنيفها ضمن أبواب تحتوي على شرح وافٍ مدعم بالصور والأمثلة.

تعريف المصفوفات

أول موضع سوف نتناوله في بحث عن المصفوفات هو تعريف المصفوفة في الرياضيات، حيث إنها عبارة عن ترتيب على هيئة مستطيل من الأرقام أو الرموز أو التعبيرات مرتبة في صفوف وأعمدة، حيث عادة ما يتم كتابة المصفوفات بين قوسين مربعين؛ وتسمى الخطوط الأفقية في المصفوفة بالصفوف، أما الخطوط العمودية في المصفوفة فتسمى بالأعمدة.

ويتم تحديد حجم المصفوفة من خلال عدد الصفوف والأعمدة التي تحتوي عليها؛ بحيث تسمى المصفوفة المكونة من العدد m من صفوف والعدد n من الأعمدة (مصفوفة m × n) وتقرأ مصفوف m في n، بينما يسمى الرقمين m و n بأبعاد المصفوفة. ويكون شكل المصفوف كالتالي: [1]

أنواع المصفوفات

هناك مصفوفات في جميع أنواع الأحجام، ولكن عادةً ما تكون أشكالها متشابهة، ويُطلق على حجم المصفوفة أبعادها وهو يمثل العدد الإجمالي للصفوف والأعمدة في المصفوفة، ولكن قد يختلف اسم المصفوفة تبعً لاختلاف أبعادها أو اختلاف عناصرها؛ حيث أن هناك عدة أنواع من المصفوفات كما يأتي: [2]

• مصفوفة الصف (Row Matrix).
• مصفوفة العمود (Column Matrix).
• مصفوفة منفردة (Singleton Matrix).
• مصفوفة مستطيلة (Rectangular Matrix).
• مصفوفة مربعة (Square Matrix).
• مصفوفات متماثلة (Identity Matrices)..
• مصفوفة الوحدة (Matrix of ones، Unit Matrix).
• مصفوفة الصفر (Zero Matrix).
• مصفوفة قطرية (Diagonal Matrix).

شاهد أيضًا: بحث عن الدوال الرئيسة الام والتحويلات الهندسية

أهمية المصفوفات

على الرغم من أن المصفوفات لها الكثير من الفائدة والتطبيقات في حياتنا إلا أن الفصول الدراسية لا تتناول سوى طرق حلها والعمليات التي تجرى عليها، لكن استخدامات المصفوفات في حياتنا كثير لهذا سوف أدرج بين هذا البحث عن الموصوفات مجموعة منها، وهي كما يأتي: [3]

• التشفير: حيث يتم استخدام م المصفوفات في التشفير من أجل خلط البيانات لأغراض أمنية لتشفير هذه البيانات التي نحتاج إليها وفك تشفيرها، حيث إن هناك مفتاحاً يساعد في تشفير وفك تشفير البيانات التي يتم إنشاؤها بواسطة المصفوفات.
• الألعاب ثلاثية الأبعاد: تستخدم المصفوفات في الألعاب ثلاثية الأبعاد من أجل تغيير الكائن في مساحة ثلاثية الأبعاد؛ حيث يتم استخدام مصفوفة ثلاثية الأبعاد للمصفوفة ثنائية الأبعاد لتحويلها إلى كائنات مختلفة حسب المتطلبات.
• الاقتصاد والأعمال: تفيد المصفوفات في دراسة اتجاهات الأعمال والأسهم والأمور الأخرى مثل إنشاء نماذج أعمال وما إلى ذلك.
• البناء: على الرغم من أن معظم المباني مستقيمة إلا أنه في بعض الأحيان يحاول المهندسون المعماريون تغيير الهيكل الخارجي للمبنى كما هو الحال في برج خليفة الشهير، وذلك يمكن القيام به باستخدام المصفوفات، كما يمكن أن تساعد المصفوفات في دعم الهياكل التاريخية المختلفة.
• إضفاء الحيوية: يمكن أن تساعد المصفوفات في جعل الرسوم المتحركة أكثر دقة وكمالًا.
• الفيزياء: يتم تطبيق المصفوفات في دراسة الدوائر الكهربائية وميكانيكا الكم والبصريات، حيث يساعد في حساب مخرجات طاقة البطارية، وتحويل المقاومة للطاقة الكهربائية إلى طاقة أخرى مفيدة.  كما تلعب المصفوفات دورًا رئيسيًا في العمليات الحسابية خاصة في حل المشكلات باستخدام قوانين كيرشوف للجهد والتيار، وأيضًا تساعد في دراسة فيزياء الكم واستخدامها.
• الجيولوجيا: حيث تستخدم المصفوفات لأخذ المسوحات الزلزالية.

خصائص المصفوفات 

تختلف خصائص المصفوفات باختلاف نوعها، فلكل نوع من المصفوفات خصائص تميزه عن غيره من المصفوفات، وفيما يأتي بعض الخصائص العامة لأنواع المصفوفات: [4]

• تنظم الأعداد والبيانات في المصفوفة بحيث يكون الموقع فيها له معنى، وتسمى كل قيمة داخل المصفوفة تحتل موقعًا معينًا بالعنصر، ويرمز للمصفوفة عادة من خلال كتابة حرف كبير تحته خط مثل: A.
• كل مصفوفة لها رتبة معينة يمكننا أن نحدد نوعها من خلالها فمثلًا عندما نقول أن رتبة المصفوفة هو 3×2 يكون عدد الأعمدة فيها 3 والصفوف 2.
• تكون المصفوفتان متساويتان إذا كانت لهما الرتبة نفسها وتساوتا في العناصر المتناظرة.
• عند تنظيم البيانات في المصفوفة يسهل تحليلها وتفسيرها، وتعطي مجموع العناصر في الصفوف والأعمدة أحيانًا قيمًا لها معنى، وفي بعض الأحيان لا يكون لها معنى حسب البيانات التي تمثلها المصفوفة.
• في المصفوفة المربعة، يكون عدد الصفوف والأعمدة متساويًا.
• المصفوفة المربعة تكون مصفوفة قطرية عندما تكون فيها العناصر غير القطرية أصفارًا.
• المصفوفة المربعة تكون مصفوفة العدد الثابت عندما تكون فيها العناصر غير القطرية أصفارًا والعناصر القطرية متماثلة.
• المصفوفة التي تكون فيها جميع العناصر غير القطرية عبارة عن أصفار والعناصر القطرية هي 1 هي مصفوفة الوحدة.
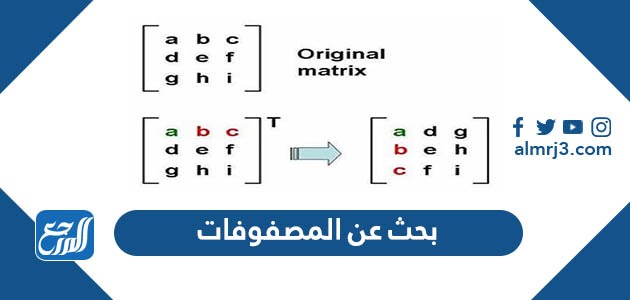
• المصفوفة تكون مصفوفة متماثلة إذا كانت A = A^T، حيث إن A^T هو مقلوب المصفوفة؛ أي عندما يتم قلب الصفوف فيها إلى أعمدة والأعمدة إلى صفوف.
• تكون المصفوفة متماثلة إذا كانت A = –A^T، حيث إن A^T هو مقلوب المصفوفة.
  المصفوفة هي مصفوفة متعامدة. إذا كان A × A^T = I، حيث I هي مصفوفة الوحدة من نفس ترتيب المصفوفة A، و A^T هو مقلوب المصفوفة.
• تسمى المصفوفة مصفوفة مفردة، إذا كان A | = 0 |
• تسمى المصفوفة مصفوفة جامدة (idempotent matrix) إذا كانت A² = A.
  تسمى المصفوفة مصفوفة إجبارية (Involutory Matrix) إذا كانت A² = I.

شاهد أيضًا: بحث عن الدوال وأنواعها كامل

مميزات المصفوفات

المصفوفات هي عبارة عن ترتيب للبيانات على شكل مستطيل لمتغيرات أو أعداد في صفوف أفقية وأخرى عمودية محصورة داخل قوسين، وباعتبار أن المصفوفة واحدة من أكثر هياكل البيانات شيوعًا في لغات البرمجة المختلفة فإن لها مميزات وعيوب، وأهم ما يميز المصفوفة ما يأتي: [5]

• تساعد المصفوفات في تحسين كتابة الكود؛ بحيث يمكننا تخزين عدد كبير من القيم في مصفوفة واحدة عن طريق كتابة جزء صغير من التعليمات البرمجية بدلاً من التصريح عن كل متغير على حدة.
• المصفوفات سهلة الاستخدام مثل العديد من الخوارزميات مثل تقنيات البحث والفرز، وإيجاد القيم القصوى والدنيا، ويمكن تنفيذ عمليات الانعكاس بسهولة باستخدام المصفوفات.
• التعقيد الزمني للوصول إلى أي عنصر من عناصر المصفوفة هو O (1)، أي أنه يستغرق قدرًا ثابتًا من الوقت للوصول إلى عنصر.
• تستخدم المصفوفات الفهارس لتحديد عناصرها، ويمكن استخدام هذه الفهارس التي تبدأ من “صفر” وتنتهي عند “طول المصفوفة – 1” للوصول إلى جميع عناصر المصفوفة.
• هناك مصفوفات ثنائية الأبعاد موجودة إلى جانب المصفوفات البسيطة تُستخدم لتخزين عناصر مصفوفة من أي أبعاد.
• المصفوفات تخزن العناصر في مواقع ذاكرة متجاورة، فلا يتم تخصيص ذاكرة إضافية خارج هذه الكتلة المجاورة، مما يمنع إهدار الذاكرة.
• المصفوفات أحد أبسط هياكل البيانات، فيمكن استخدامها لتنفيذ هياكل البيانات الأخرى مثل القوائم المرتبطة، والمكدسات، وقوائم الانتظار، والرسوم البيانية، والأشجار، وما إلى ذلك.
• يمكن استخدام المصفوفات لتنفيذ العديد من تقنيات جدولة وحدة المعالجة المركزية.

عيوب المصفوفات

عند كتابة بحث عن المصفوفات يجب ذكر عيوبها إلى جانب ميزاتها، وضمن نطاق استخدام المصفوفات في عمليات البرمجة على جهاز الحاسوب فيمكن القول أن هناك مجموعة من العيوب أو المحددات لهذه المصفوفات وهي كما يأتي: [5]

• حجم المصفوفة ثابت، وبمجرد تخصيص الذاكرة لمصفوفة، لا يمكن زيادتها أو إنقاصها، وهذا يمنعنا من تخزين بيانات إضافية في حال أردنا ذلك، وتسمى هذه المصفوفات ذات الحجم الثابت بالمصفوفات الثابتة.
• يؤدي تخصيص ذاكرة أقل من المطلوب لمصفوفة إلى فقدان البيانات.
• لا يمكن لمصفوفة واحدة تخزين قيم لأنواع بيانات مختلفة، أي أن المصفوفة متجانسة بطبيعتها.
• من الصعب جدًا تنفيذ عمليات الحذف والإدراج في المصفوفات لأنها تخزن البيانات في مواقع ذاكرة متجاورة؛ لكن من أجل التغلب على هذه المشكلة، يتم تنفيذ القوائم المرتبطة التي توفر وصولاً عشوائيًا للعناصر.

شاهد أيضًا: بحث عن علم الرياضيات

العمليات الحسابية على المصفوفات

لنستفيد من التطبيقات ونجري التطبيقات المفيدة عليها لا بد من تعلم العمليات الحسابية التي يمكن إجراؤها على المصفوفات؛ حيث إن هناك مجموعة من العمليات بما فيها عمليات الضرب والقسمة والجمع والطرح، بالإضافة إلى إيجاد معكوس المصفوفة ومحددتها، غير ذلك من العمليات المفيدة في التطبيقات المختلفة وحل المعادلات وغيرها سوف نقوم بتضمينها في هذا القسم من بحث عن المصفوفات.

جمع المصفوفات

يمكن أن نقوم بعملية جمع المصفوفات إذا وفقط إذا كانت المصفوفتان المراد إجراء العملية عليهما من الرتبة نفسها، وفي هذه الحالة يتم جمع العناصر المتناظرة. كما في المثال الآتي: [6]

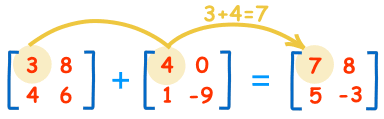
حيث إن العمليات التي تم إجراؤها هي:

• 3+4=7
• 8+0=8
• 4+1=5
• 6−9=−3

 

ولاحظنا مما سبق أن المصفوفتين يجب أن تكونا بالحجم نفسه؛ أي يجب أن تتطابق عدد الصفوف، وأن تتطابق عدد الأعمدة، وعلى سبيل المثال: يمكن إضافة مصفوفة مكونة من 3 صفوف و 5 أعمدة إلى مصفوفة أخرى تتكون من 3 صفوف و 5 أعمدة، لكن لا يمكن إضافتها إلى مصفوفة مكونة من 3 صفوف و 4 أعمدة لأن الأعمدة لا تتطابق في الحجم. [7]

سالب المصفوفة

سالب المصفوفة هو عبارة عن ضرب كل عنصر من عناصر المصفوفة بالرقم سالب واحد، والمثال الآتي يوضح:

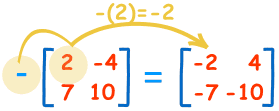
والعمليات التي تم إجراؤها من أجل إيجاد المصفوفة الناتجة هي كما يأتي:

• −(2)=−2
• −(−4)=+4
• −(7)=−7
• −(10)=−10

طرح المصفوفات

تتم عملية طرح لمصفوفتين إذا وفقط إذا كانت المصفوفتان التان نريد إجراء العملية عليهما من الرتبة نفسها، وفي هذه الحالة يتم طرح العناصر المتناظرة. وهذه العملية هي في الحقيقة عملية جمع للمصفوفة الأولى وسالب المجموعة الثانية، والمثال الآتي يوضح العملية:

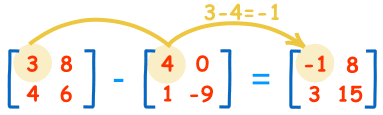
حيث إن العمليات التي تم إجراؤها كانت كما يأتي:

• 3−4=−1
• 8−0=8
• 4−1=3
• 6−(−9)=15

ضرب المصفوفات في عدد ثابت

يمكن ضرب المصفوفة بعدد ثابت وهي عملية سهلة جدًا تتم من خلال ضرب كل عنصر في المصفوفة بهذا العدد، والمثال الآتي يوضح العملية:

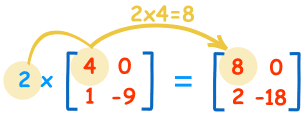
حيث إن العمليات التي تم إجراؤها على عناصر المصفوفة كانت كما يأتي:

• 2×4=8
• 2×0=0
• 2×1=2
• 2×−9=−18

ضرب المصفوفات ببعضها

ضرب المصفوفات ببعضها البعض لا يتم إلا إذا كان عدد أعمدة المصفوفة الأولى يساوي عدد صفوف المصفوفة الثانية، وعندما يتم ضرب مصفوفة رتبتها m × n بمصفوفة أخرى رتبتها r × t فإن المصفوفة الناتجة سوف تكون رتبتها m × t، والمثال الآتي سوف يوضح كيفية إجراء هذا النوع من الضرب بالتفصيل: [9]

 

يتم ضرب عناصر الصف الأول بعناصر العمود الأول، أي يتم ضرب كل عنصر مع ما يناظره من حيث الترتيب وتجمع النتائج لتوضع كأول عنصر في المصفوفة الناتجة، أي أن العمليات التي تم إجراؤها كما يأتي:
(1, 2, 3) • (7, 9, 11) = 1×7 + 2×9 + 3×11
= 58

بالمثل يتم إيجاد العنصر الثاني من المصفوفة الناتجة ويتم تكرار العملية في كل مرة، أي أننا الآن سوف نجري العمليات كما يأتي:

• نضرب كل عنصر من عناصر الصف الأول مع ما يناظره من حيث الترتيب في العمود الثاني ونجمع النواتج، لينتج معنا 64 كما يأتي:
  (1, 2, 3) • (8, 10, 12) = 1×8 + 2×10 + 3×12
  = 64
• نضرب كل عنصر من عناصر الصف الثاني مع ما يناظره من حيث الترتيب في العمود الأول ونجمع النواتج، لينتج معنا 139 كما يأتي:
  (4, 5, 6) • (7, 9, 11) = 4×7 + 5×9 + 6×11
  = 139
• نضرب كل عنصر من عناصر الصف الثاني مع ما يناظره من حيث الترتيب في العمود الثاني ونجمع النواتج، لينتج معنا 154 كما يأتي:
  (4, 5, 6) • (8, 10, 12) = 4×8 + 5×10 + 6×12
  = 154

ومن خصائص ضرب المصفوفات المصفافات ما يأتي: [8]

• إمكانية التوزيع بالشكل الآتي: A (B + C) = AB + AC
• عملية ترابطية، أي أن: A (BC) = (AB) C
• عملية تبادلية كما يأتي: (A + B) C = AC + BC
• لكل مصفوفة مصفوفة أخرى تمثل المعكوس الضربي لها إذا ضربت بها ينتج مصفوفة الوحدة وهي التي سوف أبينها في الموضوع الآتي. أي أن: A × A^T = I،

معكوس المصفوفة

من أجل إجراء عملية قسمة المصفوفات يتوجب علينا أولًا أن نجد معكوس المصفوفة، حيث أن ناتج قسمة المصفوفة A على المصفوفة B يساوي ناتج ضرب المصفوفة A بمعكوس المصفوفة B، أي (1/B). كما أننا عندما نضرب مصفوفة في معكوسها نحصل على مصفوفة الوحدة من نفس رتبة المصفوفة: [10]

والقانون المستخدم من أجل إيجاد معكوس المصفوفة هو كالآتي:

والمثال الآتي يبين طريقة إيجاد معكوس المصفوفة من خلال الخطوات:

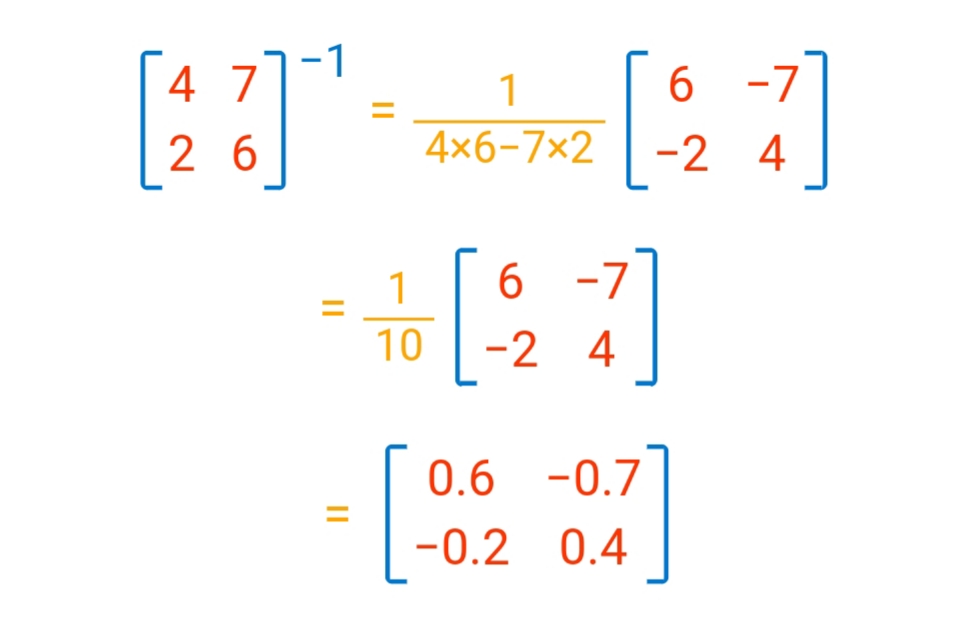
محددة المصفوفة

كل مصفوفة مربعة لها محددة وتسمى محددة المصفوفة 2 ×2 محددة الدرجة الثانية، ويمكن إيجاد محددة المصفوفة من خلال إجراء العملية الآتية: (ad-cb). والمثال الآتي يبين طريقة إجراء محددة المصفوفة:

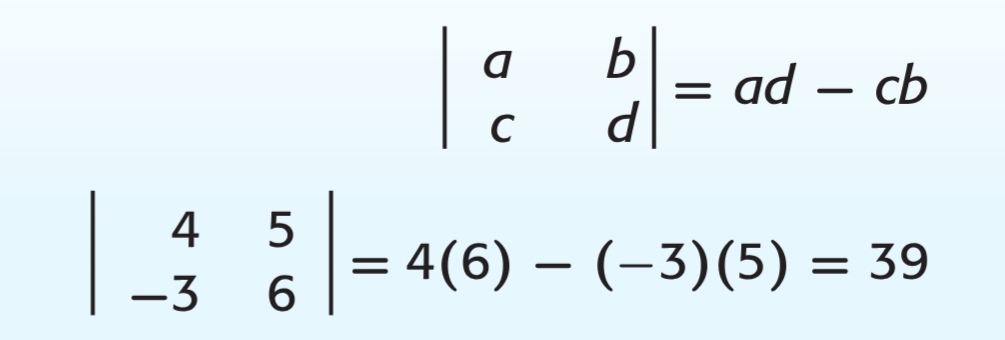
شاهد أيضًا: بحث عن الطرائق العلمية في الكيمياء

تدريبات متنوعة حول المصفوفات

من أجل تعلم المصفوفات وما يجري عليها من عمليات يجب ممارسة التمارين التي تقوي الإلمام بكل المهارات المتعلقة بها، وفيما يأتي تدريبات متنوعة حول المصفوفات والعمليات الأساسية عليها:

شاهد أيضًا: بحث عن الكيمياء الكهربائية كامل

خاتمة بحث عن المصفوفات في الرياضيات

الآن وأنا في صدد إنهاء هذا البحث الذي تناولت فيه الحديث عن المصفوفات لا بد من التأكيد على أهمية هذا العلم في حل المعادلات بطريقة بسيطة تسهل على الطلاب إنجاز التمرينات بسرعة كبيرة، كما أنه لا بد من تسليط الضوء على المصفوفات لفائدتها الكبيرة في التقنيات الحديثة وفي لغات البرمجة المختلفة من ضمنها c++، كما يتم استخدامها لتخزين البيانات؛ فنحن عندما نتعامل مع مجموعة مرتبة من البيانات، فإن المصفوفات هي الخيار الأول والأهم لتخزين هذه البيانات، ويمكن استخدام المصفوفات لتخزين البيانات من الأنواع المختلفة مثل الأعداد الصحيحة، والأعداد العشرية، والحروف وغير ذلك من البيانات.

بحث عن المصفوفات doc

بعد أن تحدثنا فيما سبق عن المصفوفات وتناولنا العديد من الموضوعات المهمة ذات العلاقة المباشرة بالمصفوفات بدءًا من تعريفها، ثم ذكرنا أهم خصائص المصفوفات وأنواعها، وبينّا أن خصائص كل مصفوفة تختلف من خلال الاختلاف في نوعها، وبينّا أهم مميزات المصفوفة وعيوبها ضمن نطاق الحديث عن المصفوفات في البرمجة والتقنيات الحاسوبية الحديثة، ومن ثم بينّا أهم العمليات التي يمكن إجراؤها على المصفوفات من الجمع والطرح والضرب والقسمة، كما بينّا طريقة إيجاد معكوس المصفوفة ومحددتها، ويمكنكم “من هنا” تحميل بحث عن المصفوفات doc يتضمن كل هذه الفقرات.

شاهد أيضًا: بحث عن الرياضيات كامل

بحث عن المصفوفات pdf

عادة ما يتم كتابة الأبحاث من خلال برامج المايكروسوفت خاصة برنامج الوورد الذي يتيح إمكانية كتابة الأبحاث وإجراء التعديلات عليها بكل أنواعها بما فيها أبحاث الرياضيات التي تتضمن نماذج جاهزة من المعادلات والمصفوفات والعمليات الرياضية يمكن استخدامها، بالإضافة إلى إمكانية إدراج الصور التوضيحية، ومن ثم يتم تخزين البحث بصيغة pdf من أجل الاحتفاظ بالمعلومات المكتوبة ضمن فقرات وما عليها من تعديلات. ويمكنكم “من هنا” تحميل بحث عن المصفوفات pdf والاستفادة منه.

وفي الختام، نكون قد أدرجنا لكم بحث عن المصفوفات في الرياضيات كامل يتضمن العديد من الفقرات القيمة التي يمكنكم الاستفادة منها عند إعداد البحث الخاص بكم عن المصفوفات بالصيغتين doc  و pdf لأنهما الصيغتين الأساسيتين اللتين يتم طلب البحث فيهما عادةً.