بحث عن الدوال وأنواعها كامل

بحث عن الدوال وأنواعها كامل من الأبحاث التي تعد تتحدث عن القسم الأهم من علم الجبر، حيث أن علم الجبر علم متنوع لأنه لا يتعامل مع الأرقام فحسب وحساباتها والعمليات التي تجري عليها، بل هو علم واسع يشمل المتغيرات والأرقام والرموز والعلاقات التي تربطها ببعضها البعض. ولأن موقع الموجع يقع في طليعة المواقع العربية التي تقدم للطلاب أبحاثًا مميزة تساعدهم على الدراسة بكفاءة عالية، فإننا في هذا المقال سوف درج لكم نموذج بحث شامل عن الدوال بأنواعها والعمليات التي يمكن إجراؤها عليها.

مقدمة بحث عن الدوال

بسم الله الرحمن الرحيم، والحمد لله ربّ العالمين الذي منّ علينا بأن علمنا بعد أن لم نكن نعلم، والصلاة والسلام على معلمنا وهادينا ونبينا المصطفى وعلى آله وصحبه أجمعين، أما بعد:

أبدأ كتابة هذا البحث عن الدوال، وهو يعد من أهم موضوعات علم الرياضيات، لما له من أهمية بالغة؛ حيث أن من تعلم الدوال والعمليات التي يمكن إجراؤها عليه كان ذلك مدخلًا له لفهم الكثير من موضوعات الرياضيات المتقدمة؛ من النهايات، وحل المعادلات التفاضلية والاشتقاقات، بالإضافة إلى حل التكاملات، وما عليها من تطبيقات تعد مهمة جدًا في العلوم الأخرى؛ حيث إن لها تطبيقات واسعة تتعلق في الفيزياء والكيمياء، والطب، والهندسة، وغيرها، كما يمكن من خلالها تمثيل الكثير من الظواهر الكونية.

بحث عن الدوال وأنواعها كامل

سوف أتناول في هذا البحث مجموعة من الموضوعات المهمة التي تتعلق بالدوال والعمليات عليها؛ حيث سوف تكون مصنفة بالطريقة التدريجية في أبواب، بالشكل الآتي:

• الباب الأول: تعريف الدوال، مع مثال على الدوال بالصور والكتابة.
• الباب الثاني: أنواع الدوال الأم وما يتفرع منها، بما فيها:
  • كثيرات الحدود ودوالها؛ بما فيها الدالة الثابتة، والدالة الخطية؛ مع ذكر فرعيها المحايدة، والمتناقصة، والدالة التربيعية، الدالة التكعيبية.
  • الدالة النسبية؛ والتي تمثل الاقترانات الكسرية.
  • دالة أكبر عدد صحيح، أو ما يسمى بالدالة الدرجية.
  • الدالة الأسية واللوغاريتمية، بالإضافة إلى الدالة الجذرية.
  • الدالة المتعددة، وطريقة كتابتها وتمثيلها بالتفصيل.
  • الدوال المثلثية وقوانيها.
• الباب الثالث: توضيح مفهوم الدوال الزوجية والفردية.
• الباب الرابع: العمليات على الدوال وتركيب دالتين.

تعريف الدوال

الدوال في الرياضيات تمثل تعبير أو قاعدة أو قانون يحدد علاقة بين متغير واحد الذي يعرف بالمتغير المستقل، ومتغير آخر؛ وهو ما يعرف بالمتغير التابع. والدوال التي تستخدم بشكل واسع في الرياضيات ضرورية جدًا لتوضيح العلاقات الفيزيائية والتطبيقات المختلفة في العلوم. وقد تم تقديم التعريف الحديث للدالة لأول مرة في عام 1837م من قبل عالم الرياضيات الألماني بيتر ديريتشليت. [1]

وقد كان التعريف هو: “إذا كان المتغير y مرتبطًا بمتغير x، فحينما يتم تعيين قيمة عددية لـ x، يتم تحديد قيمة معينة وفريدة لـ y من خلال قاعدة يتم ذلك بموجبها، وعندئذٍ يُقال إن y هي دالة للمتغير المستقل x”. ويُرمز إلى هذه العلاقة عادةً كـ y = f (x) التي يُقال عنها باللغة الإنجليزية “f of x”، بحيث لا يمكن أن تحتوي f (x) على أكثر من قيمة واحدة لنفس x.

شاهد أيضًا: بحث عن الخوارزمي كامل

مثال عن الدوال

كما ذكرنا سابقًا الدوال هي العلاقات التي تربط المتغير المستقل x بالمتغير التابع y والذي يقال له f (x)، بحيث ترتبط كل قيمة ل (x) بقيمة واحدة ل f (x)، وتسمى القيم التي يمكن تعويضها في المتغير (x) المجال، بينما تسمى القيم الناجمة عنها (قيم f (x) بالمدى. ونضع لكم في الصورة الآتية مجموعة من الأمثلة على الدوال:

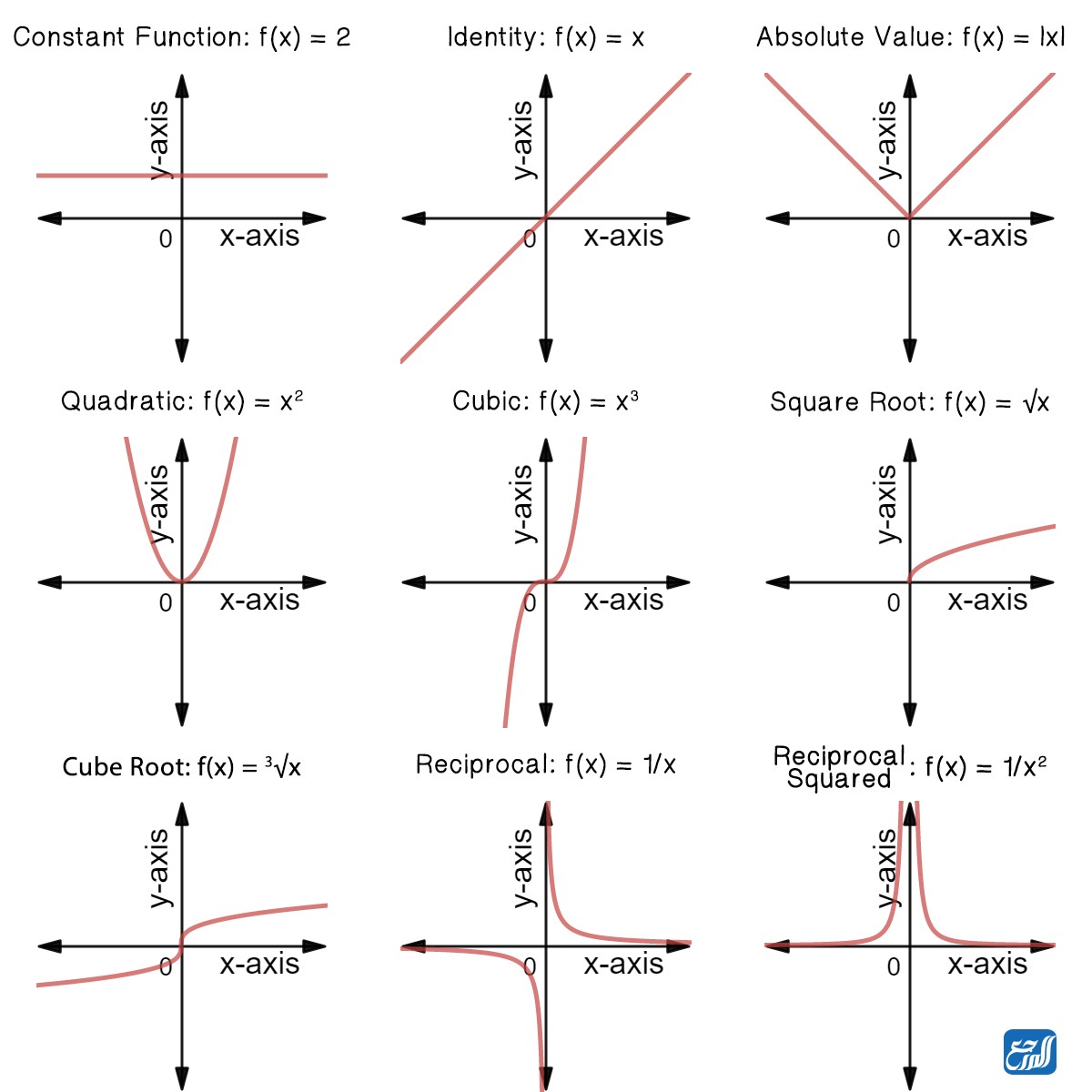
أنواع الدوال

الاقترانات هي عبارة عن علاقات بين المتغيرات والرموز، بحيث أن عناصر المجال ترتبط بعناصر المدى بعلاقة معينة، وما يميز الدوال عن العلاقات هو أن كل عنصر في المجال يرتبط بعنصر واحد فقط في المدى، بخلاف العلاقة الرياضية، وهناك أنواع متعددة للدوال كما يأتي:

• كثيرات الحدود: ومن أشهرها:
  • الدالة الثابتة.
  • الدالة الخطية.
  • الدالة التربيعية.
  • الدالة التكعيبية.
• الدوال الأسية.
• الدوال اللوغاريتمية.
• الدوال الدائرية.
• دالة أكبر عدد صحيح.
• دالة القيمة المطلقة.
• الدالة المتعددة.
• الدالة النسبية، والكسرية.
• الدالة الجذرية.

كثيرات الحدود ودوالها

كثيرات الحدود هي الاقترانات التي تكون صورتها الأساسية بالشكل الآتي: أ_ن س ^ن + أ_ن-1 س ^ن-1 +أ_ن-2 س ^ن-2 +……. أ₀ حيث أ_ن لا يساوي صفر، ون تنتمي إلى الأعداد الطبيعية، وتسمى أ_ن ^، أ_ن-1 ، أ_ن-2 ^، ……. أ₀ ، والمعامل الأول منها وهو أ_ن هو المعامل الرئيسي في الدالة. وكثير الحدود الذي تكون جميع معاملاته أصفار بالاقتران الصفري، وهو (f (x) = 0) وهذا ليس له درجة، ويمثله المحور x في المحور الديكارتي. [2]

كما أن مجال الاقتران كثير الحدود هو مجموعة الأعداد الحقيقية، ومداه هو مجموعة الأعداد الحقيقية أو مجموعة جزئية منها حسب نوع الاقتران كما سوف يتم توضيحه فيما يأتي. ويتم تحديد درجة كثير الحدود ونوعه وفقًا للأس الأكبر في الدالة، وسوف نبين لكم فيما يأتي أنواع الاقترانات كثيرة الحدود. والصورة الآتية تبين التمثيل البياني العام لأنواع مختلفة من كثيرات الحدود، مع التنبيه على ملاحظة أن درجة كثير الحدود تعبر عن عدد المقاطع السينية له كما هو مبين في الشكل:

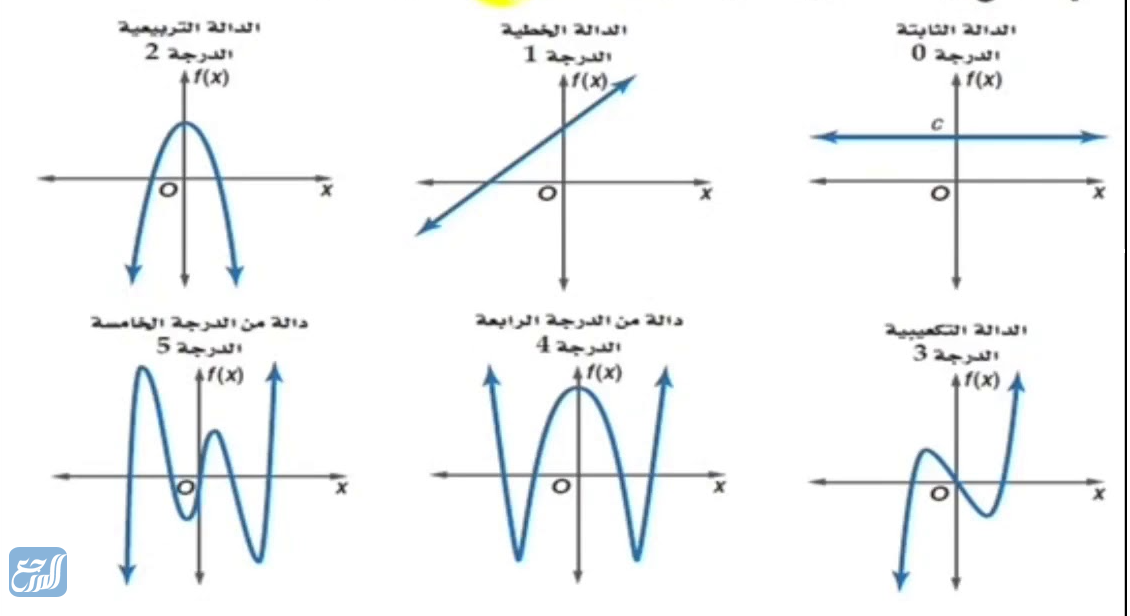
الدالة الثابتة

الدالة الثابتة هو النوع الأول والأبسط من أنواع الاقترانات الحدود، وهي عندما تكون درجة كثير الحدود هي الصفر، أي أن أس (س) فيها يساوي صفر، وأي رقم مرفوع للقوة صفر تكون النتيجة له هي واحد، وبالتالي عندما يضرب بأي رقم سوف تكون النتيجة هي الرقم نفسه. وسوف نوضع ذلك فيما يأتي، مع البيان التمثيلي للدالة الثابتة.

f(x) = x⁰ * a
f(x) = 1* a
f (x) = a، حيث إن a هو أي رقم حقيقي.
على سبيل المثال: (f (x) = 3)

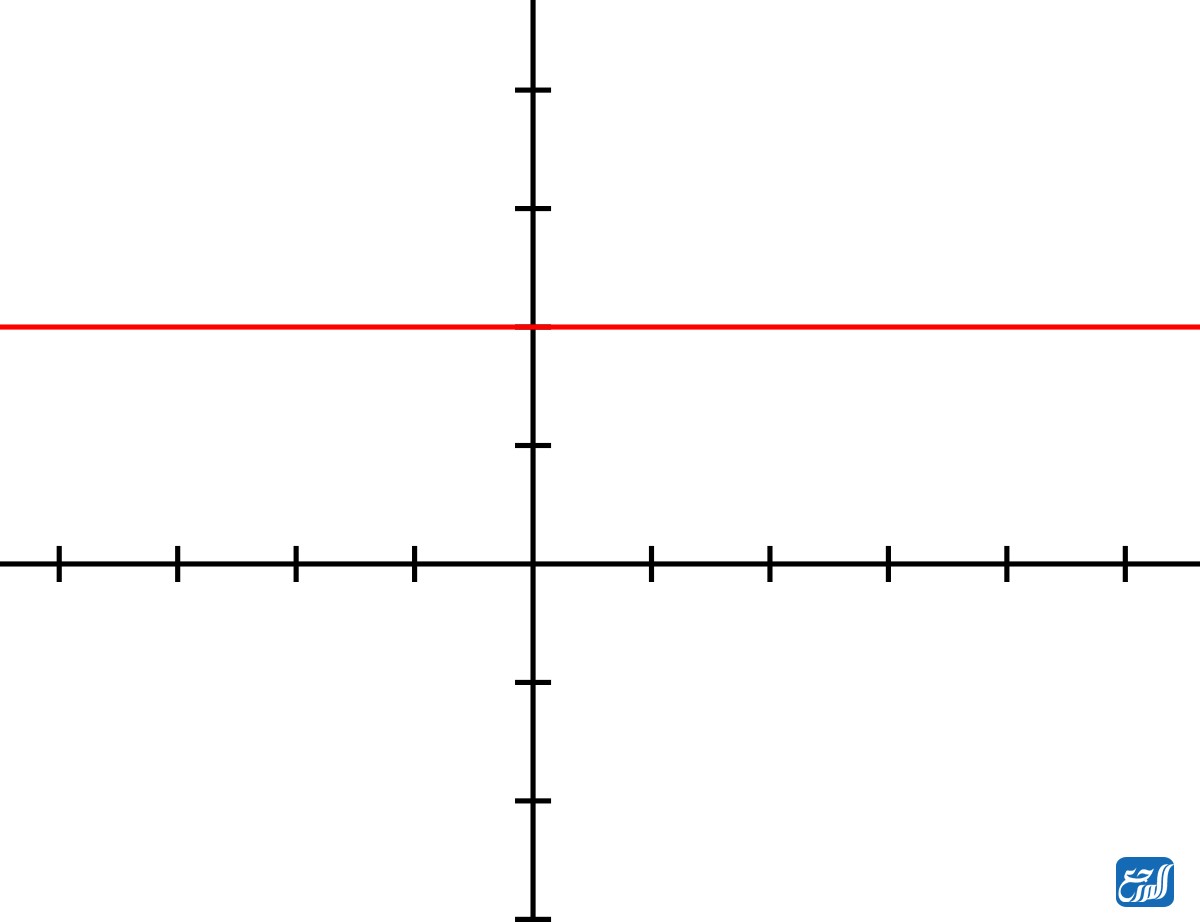
الدالة الخطية

الدالة الخطية هي الدرجة الأكبر من الدالة الثابتة، وفيها يكون أس المتغير (س) هو واحد، وتكون صيغتها العامة هي: (f (x) =ax +c)، وفيما يأتي توضيح للصيغة: [3]

f(x) = ax¹ + c ، x¹ = x ،
وبالتالي: f(x) = ax + c

والطريقة الأبسط لرسم الدالة الخطية هي من خلال أخذ نقطتين تمثلان أي رقمين حقيقين والتمثيل بينهما، لكن للحصول على نتيجة أكثر دقة يمكن أن نأخذ 5 نقاط اثنان منها في الموجب واثنان في السالب وواحد صفر، ومن ثم تعويضهما في الاقتران، ووضع النقاط على الرسم البياني بشكل (س، ص)؛ أي كل رقم تم تعويضه مع إجابته ومن ثم التوصيل بين النقاط، كما في الشكل الآتي:

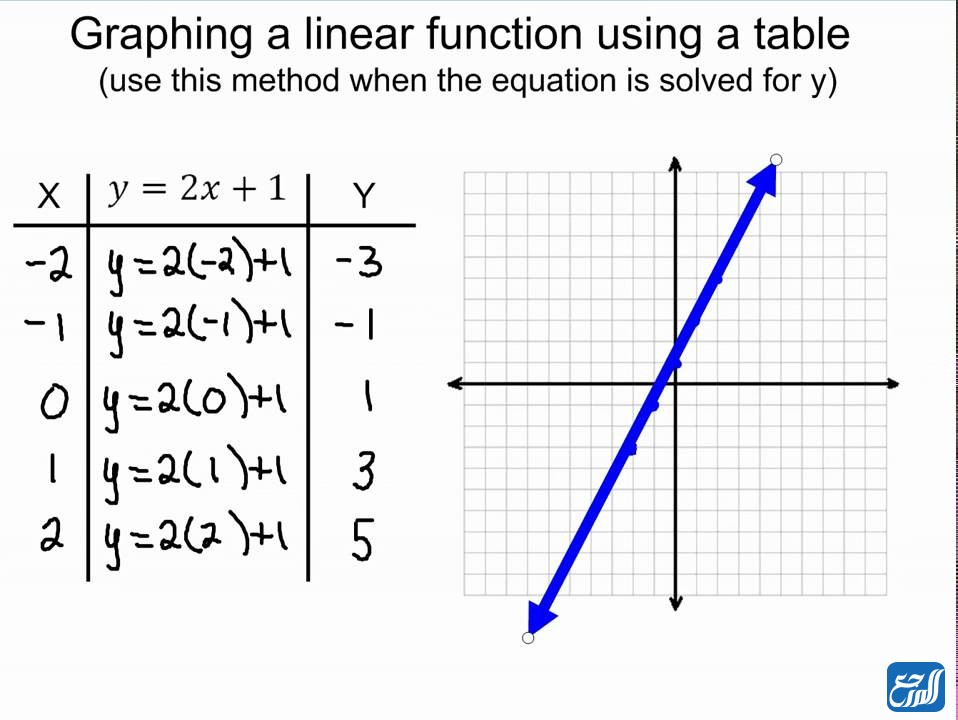
الدالة الخطية المتناقصة

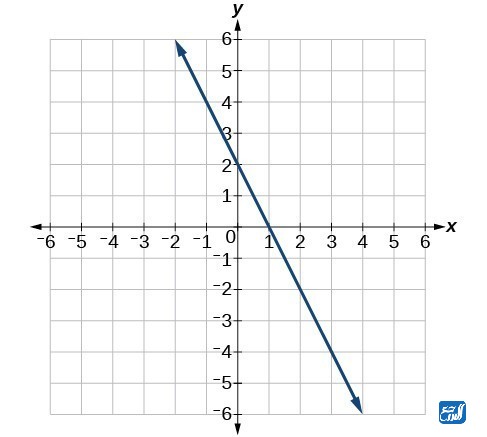
تعد الدالة الخطية المتناقصة فرع من الدالة الخطية، وقد سميت بهذا الاسم لأن الخط الذي يمثلها على الرسم البياني سوف ينحدر إلى الأسفل كلما زدنا قيم (x)، أي أن صورة الاقتران (f (x) سوف تقل مع زيادة الرقم الذي يتم تعويضه مكان (x) في كل مرة، وفي هذه الحالة يكون معامل (x) سالب، مثل: (f (x) = -2x + 1) أو (f (x) = -x).

إذا أخذنا (f (x) = -x) على سبيل المثل وأبرزنا نتائج تعويض أرقام مختلفة مكان (x) سوف نحصل على النتيجة الآتية:

• عند تعويض الرقم 1 سيكون الناتج هو -1.
• عند تعويض الرقم 2 سيكون الناتج هو -2.
• عند تعويض الرقم 3 سيكون الناتج هو -3.
• عند تعويض الرقم 4 سيكون الناتج هو -4، وهذا كلما زادت قيمة (x) قلت قيمة f (x).

الدالة المحايدة

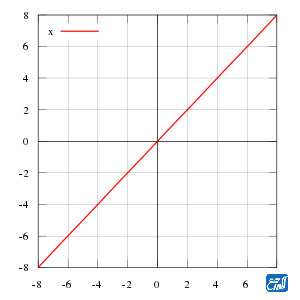
الدالة المحايدة أيضًا فرعًا عن الدالة الخطية، وهي الدالة الخطية التي يكون فيها قيمة (x) مساوية لقيمة (f (x) عند التعويض والتمثيل البياني، وتكون صورتها هي: (f (x) = x) دائمًا، وقد سمي بالاقتران المحايد أو الدالة المحايدة إلى قيمة المتغير وصورته متساوية وواحدة دائمًا. وعلى سبيل المثال سوف تكون نتائج تعويض الأرقام فيها كما يأتي:

• عند تعويض الرقم 1 سيكون الناتج هو 1.
• عند تعويض الرقم 2 سيكون الناتج هو 2.
• عند تعويض الرقم 3 سيكون الناتج هو 3.
• عند تعويض الرقم 4 سيكون الناتج هو 4، أي أن قيمة (x) مساوية لقيمة (f (x) دائمًا.

الدالة التربيعية

الدالة التربيعية تعد أيضًا شكلًا من أشكال متغيرات الحدود، ويكون فيها درجة الاقتران أو الدالة هي الثاني، أي أن المتغير الأساسي فيها مرفوع للقوة 2، وصورته هي (f(x) = ax² +bx + c) ويقطع هذا التمثيل منحنى السينات مرتان، ويتم رسم التمثيل البياني له بكل سهولة من خلال إيجاد ثلاث نقاط؛ الأولى والثانية هما أصفار الاقتران والثالثة هي قمة المنحنى وما يسمى بصورة رأس القطع التي ينقسم عندها المنحى إلى نصفين متماثلين، وفيما يأتي سوف نوضح لكم طريقة رسم المنحنى التربيعي بالخطوات:

على سبيل المثال: (f(x) = x² – 1)
له مقطعان سينيان يتم إيجادهما كما يأتي:
نضع مكان f (x) الرقم صفر فيصبح الاقتران على صورة معادلة كما يأتي: 0 = x² – 1
نحل المعادلة، إما بنقل الرقم (1) إلى الجهة الأخرى من المعادلة، ثم وضع جذر للطرفين كما يأتي:
1 = x2 ، بوضع الجذر التربيعي للطرفين نحصل على:
1 – = x و 1 = x
أو يمكن حلها من خلال تحليل فرق بين مربعين كما يأتي:
0 = x² – 1
0 = (x – 1) (x + 1)
1 – = x و 1 = x، وفي الحالتين نحصل على نفس النتيجة.

رأس القطع: وهي النقطة الثالثة، فيمكننا إيجادها من خلال التعويض في (b/ 2*a-)، فيكون الناتج كما يأتي:
( b/ 2*a-) = (0/ 2*1-) = 0 ، حيث أن الحد الأوسط غير موجود وبالتالي (b=0). فتكون قيمة رأس القطع في كل الحالات التي ليس لها حد أوسط من الاقتران التربيعي هي صفر، ولا حاجة في هذه الحالة إلى التعويض.
صورة رأس القطع فهي: (f(x) = 0² – 1)
f(x) =-1

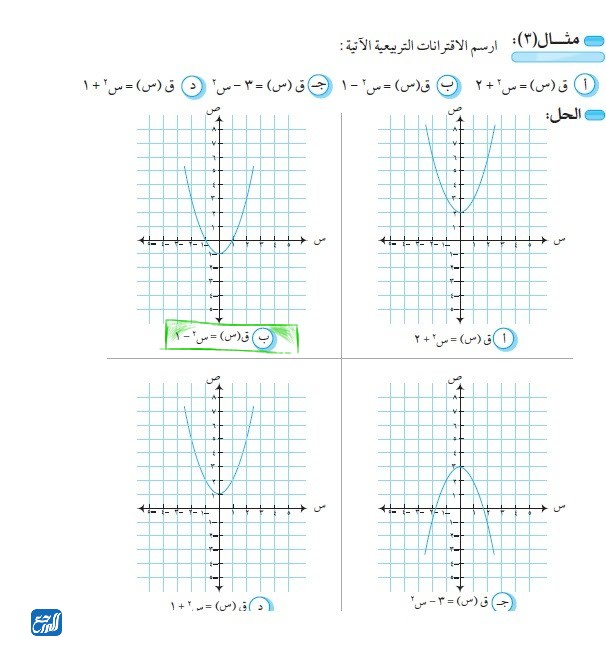
وهكذا نكون حصلنا على ثلاث نقاط هي المقطعان السينيان ورأس القطع وهي على التوالي: (0,1)، (-0,1)، (1,0-)، ونعوضها على المحور الديكارتي لنحصل على التمثيل البياني، وهو الرسمة اليمنى العليا في الشكل الآتي (كما هو محدد عليها في اللون الأخضر) الذي يمثل مجموعة من التمثيلات البيانية لاقترانات متعدد يمكنكم الاستفادة منها:

الدالة التكعيبية

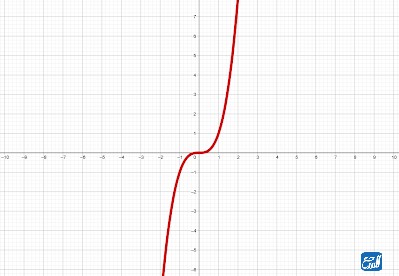
تعد الدالة التكعيبية واحدة من الدوال المتفرعة من كثيرات الحدود، وهناك دوال أعلى منها أيضًا، ولكننا سوف نقتصر في هذا البحث إلى الحديث عن الدالة التكعيبية، وهي التي تكون درجة الاقتران بها هي الثالثة تبعًا للأس، حيث أن أكبر (x) فيها مرفوعة للأس 3، وتكون الصورة القياسية لها كما يأتي: (f(x) = ax³ +bx² + cx+ d).

ولهذا الاقتران ثلاثة مقاطع سينية، ويمكن تمثيل من خلال تعويض مجموعة من القيم في الاقتران، لكن للحصول على دقة أكبر يمكن تمثيلها من خلال برنامج الإكسل أو تطبيقات الرسم المتاحة، حيث أن الاقتران التكعيبي وما هو أعلى منه بالدرجة يعد رسمه صعبًا بعض الشيء بالطريقة الاعتيادية اليدوية. وسوف نضع لكم تمثيلًا بينيًا للاقتران التكعيبي فيما يأتي:

الدالة النسبية

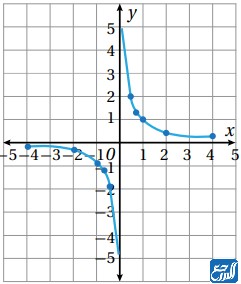
الاقترانات النسبية هي نوع جديد من الدوال، وهي عبارة عن اقتران يمكن كتابتها بصورة نسبية بين كثيري حدود، مثل (f (x) /g (x)، بشرط أن g (x) لا يكون مساويًا للصفر. ومجال الاقتران النسبي هو مجموعة الأعداد الحقيقية عدا ما يجعل المقام مساويًا للصفر، ولإيجاد المجال نحلل كثير الحدود الموجود في المقام من أجل إيجاد الأصفار. وفيما يأتي نبين لكم طريقة مجال الاقتران النسبي مع مثال:

المثال: (f(x) = (x + 2)/(x² – 9
ومن أجل إيجاد مجال الاقتران النسبي نحلل كثير الحدود الموجود في المقام من خلال تحويل الاقتران إلى معادلة عن طريق وضع رقم (0) مكان f (x) كما يأتي: 0 = x² – 9، فتكون لدينا طريقتان لحل المعادلة كما يأتي:

• نقل الرقم (9) إلى الجهة الأخرى من المعادلة، وبعدها نضع الجذر التربيعي للطرفين كما يأتي:
  9 = x² ، ثم نضع جذرًا تربيعيًا للطرفين ونحصل على:
  3 – = x و 3 = x
• تحليل فرق بين مربعين، بالطريقة الآتية:
  0 = x² – 9
  0 = (x – 3) (x + 3)
  3 – = x و 3 = x ،

وفي الطريقتين سوف نحصل على نفس النتيجة، أي أن أصفار المقام هما {3، -3}، فيكون المجال هو: ح – {3، -3}.

شاهد أيضًا: بحث عن علم الرياضيات

الدالة الدرجية (اقتران أكبر عدد صحيح)

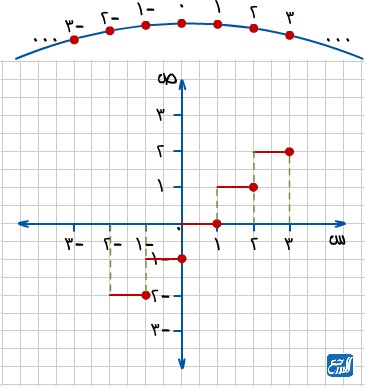
اقتران أكبر عدد صحيح، أو الدالة الدرجية تعد واحدة من أنواع الدوال الحقيقية، وهو الاقتران f الذي يقرن كل عدد حقيقي صحيح أقل من أو يساوي x، ويرمز له بالرمز [x]. وبشكل عام فإنه إذا كان n≤x<n+1 ، حيث إن n عدد صحيح، فإن f(x) = [x] = n

وعند تعويض قيم متعددة في الاقتران f(x) = [x] سوف نحصل على ما يأتي:

• عند تعويض الرقم -1 سيكون الناتج هو -1.
• عند تعويض الرقم 4 سيكون الناتج هو 4.
• عند تعويض الرقم 1.8 سيكون الناتج هو 1.
• عند تعويض الرقم -2.5 سيكون الناتج هو -3.

ويكون التمثيل البياني كما هو موضح بالشكل الآتي:

 الدالة الاسية

يسمى الاقتران المعرف بالقاعدة f(x) = a * b^g(x) +c بالاقتران الأسي، حيث أن g(x) اقتران حقيقي وباقي الرموز a و b و c جميعها أعدادًا حقيقية، a لا تساوي صفر، b أكبر من صفر، حيث أن g(x) يسمى أس، والرمز b هو الأساس في الاقتران f(x).  [4] وسوف نضع لكم فيما يأتي رسمًا يمثل الاقتران الأسي f(x) = a^x :

لرسم الاقتران f(x) = 2^x نعوض مجموعة من القيم كما يأتي:

• عند تعويض الرقم -2 سيكون الناتج هو (1/4). فتتكون النقطة (-2، 1/4).
• عند تعويض الرقم -1 سيكون الناتج هو (1/2). فتتكون النقطة (-1، 1/2).
• عند تعويض الرقم 0 سيكون الناتج هو 1. فتتكون النقطة (0، 1).
• عند تعويض الرقم 1 سيكون الناتج هو 2. فتتكون النقطة (1، 2) 1.
• عند تعويض الرقم 2 سيكون الناتج هو 4. فتتكون النقطة (2، 4).

وبعدها نرسم المستوى الإحداثي ونضع عليه النقاط التي قمنا بإيجادها مسبقًا، وأخيرًا نصل بينها بخط، فتصبح كما في الشكل الآتي:

 

الدالة اللوغاريتمية

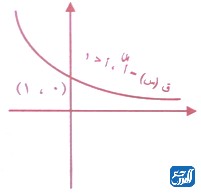
إذا كانت س> صفر، أ> صفر، أ لا يساوي 1، فإن f(x) =log_a (x)، وذلك إذا وفقط إذا كانت x = a^f(x)، ويسمى الاقتران المعرف بالقاعدة log_a (x)= f(x) بالاقتران اللوغاريتمي، حيث إن a هو أساس اللوغاريتم. وسو نبين فيما يأتي مجموعة من التطبيقات على اللوغاريتمات.

• مثال: log₃ (81)
  الإجابة: 4
• مثال: log₅ (125)
  الإجابة: 3

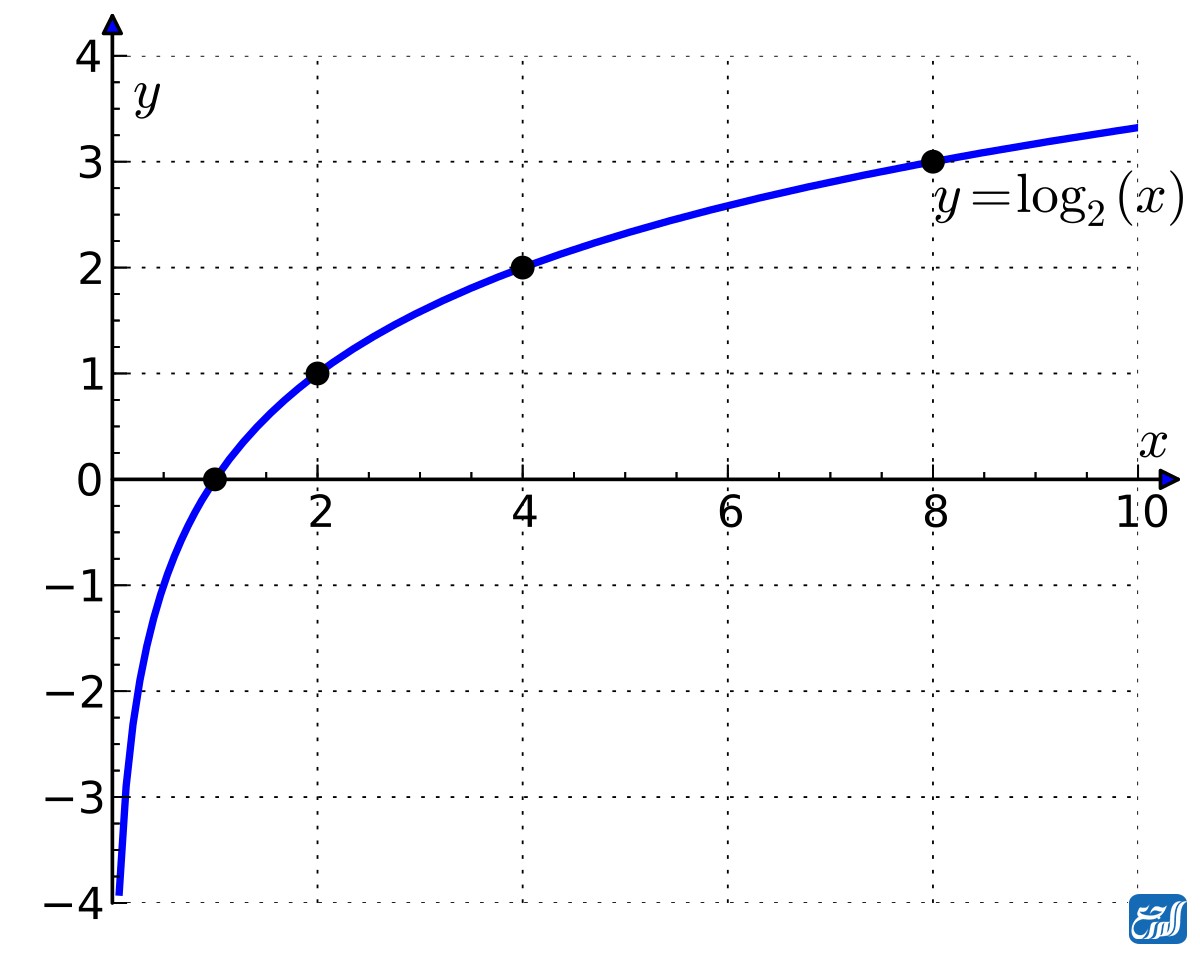
ولرسم الاقتران البياني f(x) =log₂ (x) نعوض مجموعة من النقاط في الاقتران كما يأتي ثم نضع النقاط على الرسم البياني ونصل بينها بخط منحني فينتج معنا الرسم أدناه:

• عند تعويض الرقم (1/4) سيكون الناتج هو -2. فتتكون النقطة (1/4، -2).
• عند تعويض الرقم (1/2) سيكون الناتج هو -1. فتتكون النقطة (1/2، -1).
• عند تعويض الرقم 1 سيكون الناتج هو 0. فتتكون النقطة (1، 0).
• عند تعويض الرقم 2 سيكون الناتج هو 1. فتتكون النقطة (2، 1).
• عند تعويض الرقم 4 سيكون الناتج هو 2. فتتكون النقطة (4، 2).

شاهد أيضًا: بحث عن الطرائق العلمية في الكيمياء

الدالة الجذرية

الاقترانات الجذرية نوع من الاقترانات الحقيقية والتي تكتب بالصيغة الآتية: f(x) = √g(x). حيث إن هـ اقتران كثير الحدود. ولرسم هذا النوع من الاقترانات نحتاج إلى تحديد مجال الاقتران ثم إيجاد بعض صور لمجموعة من عناصر المجال ونمثلها في المستوى البياني، ثم نوصل بين النقاط بخط منحني. حيث يكون مجال هذا الاقتران جميع القيم التي تجعل ما تحت الجذر أكبر من أو يساوي صفر. وسوف نضع لكم فيما يأتي مثال يوضح طريقة إيجاد المجال والرسم البياني:

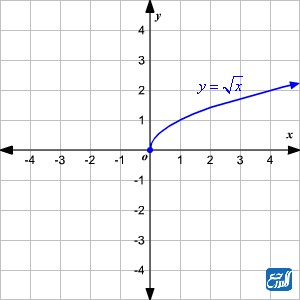
مثال: f(x) = √x ، جد مجال الاقتران مع رسم المنحنى: 

لإيجاد المجال نجعل ما تحت الجذر على شكل متباية أكبر أو يساوي صفر كما يأتي:
x≥0 ، فيكون المجال هو { x: x ∈ R، x≥0} = [0 ، ∞)
ويمكننا الآن تعويض بعض القيم في الاقتران من أجل رسم الاقتران بالتمثيل البياني على المنحنى الديكاتي كما يأتي:

• عند تعويض الرقم 0 سيكون الناتج هو 0.
• عند تعويض الرقم 1 سيكون الناتج هو 1.
• عند تعويض الرقم 4 سيكون الناتج هو 2.
• عند تعويض الرقم 9 سيكون الناتج هو 3.

فيكون التمثيل البياني كما يأتي:

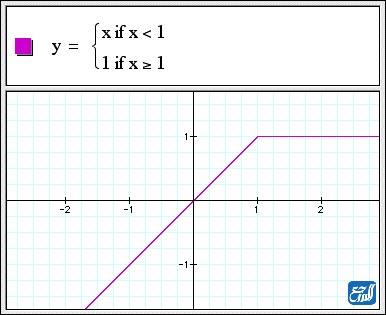
الدالة المتعددة (الاقتران المتشعب)

الاقتران المتشعب هو الاقتران الذي يكون له أكثر من قاعدة، ولكل قاعدة مجال معين، بحيث تتغير قاعدة المجال عند نقاط معينة تسمى هذه النقاط بنقاط التشعب. وفيما يأتي سوف نضع صورة تبين الاقتران المتشعب مع نموذج للرسم البياني له.

شاهد أيضًا: بحث عن الرياضيات كامل

الدوال المثلثية في المثلثات القائمة الزاوية

تعد الاقترانات الدائرية نوعين الاقترانات التي تسمى بالاقترانات الدورية، أي الاقترانات التي تكرر نفسها بشكل دوري، وهي الاقترانات التي تتضمن الجيب وجيب التمام والظل للمتغير (x)، فتكون بإحدى الصور الآتية:

• ((f(x) = sin (g(x
• ((f(x) = cos (g(x
• ((f(x) = tan(g(x

وفيما يأتي نبين لكم رسومًا بيانية للدوال المثلثية:

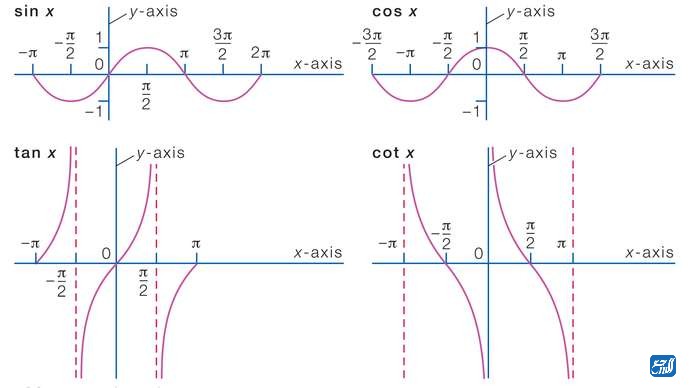
قوانين الدوال المثلثية

هناك قوانين تحكم الاقترانات الدائرية تساعد في حل النهايات، والاشتقاقات التفاضلية وحل مسائل التكامل، وهذه القوانين نشأت بعد أن تم اشتقاقها بطرق يصل بعضها إلى درجة من التعقيد، وفيما يأتي سوف نبين لكم هذه القوانين، أو ما يسمى بالمتطابقات المثلثية:

شاهد أيضًا: بحث عن الفطريات وطرق تكاثرها

الدالة الزوجية والفردية

هناك نوعين من الدوال حسب تغير قيمة الاقتران عند عكس إشارة المتغير الذي يتم تعويضه، وهما الدوال الزوجية والفردية؛ حيث إن الدالة الزوجية هي عندما يكون f(-x) = f(x)، أي أن قيمة الاقتران لا تتغير عند تعويض قيمة x سواء كانت بقيمة موجبة أو سالبة في مجال f(x). أما الدوال الفردية فهي عندما تكون f(-x) = -f(x)؛ أي عندما تتغير قيمة الدالة في حالة تعويض x بقيمة سالبة بحيث تكون القيمة الناتجة عكس قيمة الدالة الأصلية لجميع قيم x في مجال f(x).

ومن الأمثلة على الدوال الزوجية: [5]

• الدالة التربيعية عندما يكون الاقتران مكون من المتغير الأساسي فقط مثل: f(x) = x²، وأي كثير حدود مرفوع لأس زوجي.
• دالة جيب التمام.
• دالة القاطع (قا).

ومن الأمثلة على الدوال الفردية:

• أي دالة من كثيرات الحدود تكون مكونة من المتغير الأساسي فقط مثل: f(x) = x⁵ ، f(x) = x³ ، f(x) = x ….
• دالة الجيب.
• دالة الظل (ظا).
• دالة ظل التمام (ظتا).
• دالة قاطع التمام (قتا).
• الدالة العكسية للجيب.
•  الدالة العكسية للظل.

شاهد أيضًا: بحث عن المناطق الحيوية البرية كامل بالصور

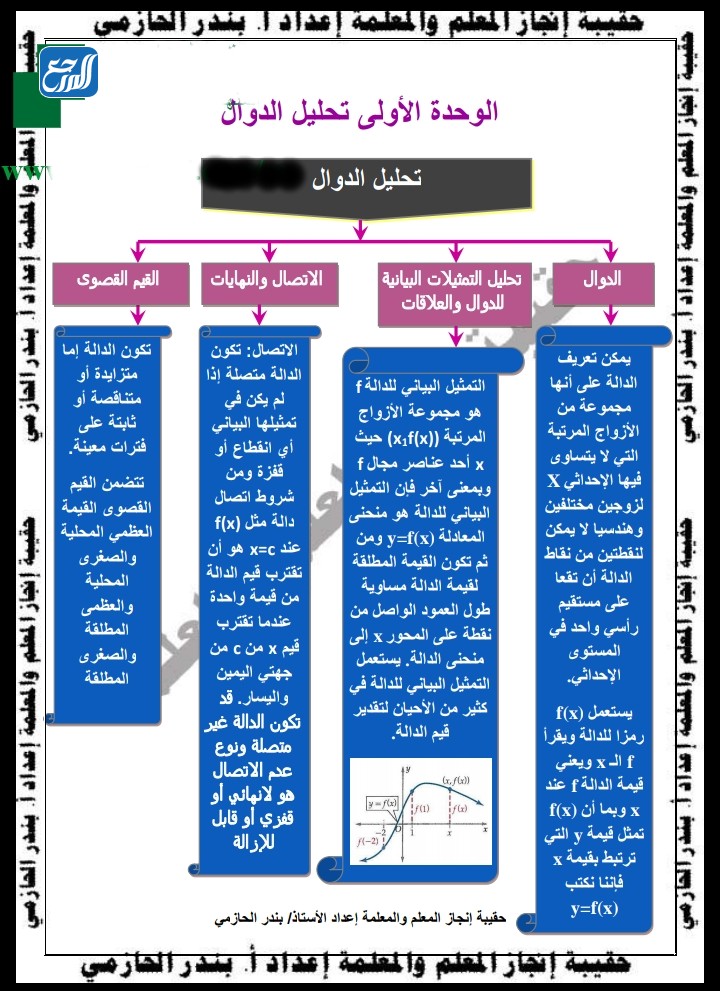
خريطة مفاهيم تحليل الدوال

يعتمد الكثير من الطلاب على خرائط المفاهيم من أجل تسهيل فهم الأمور وحفظها، لهذا يمكن للصورة الآتية التي تمثل خريطة مفاهيم تحليل الدوال أن تفيد الطلاب:

شاهد أيضًا: بحث عن شبكات الحاسب

العمليات على الدوال وتركيب دالتين

لتتأكد الفائدة المرجوة من تعلم الدوال لا بد من تعلم العمليات التي يمكن إجراؤها على الدوال، وأيضًا تركيب الدوال والدوال العكسية بصفتها نوع من العمليات التي يتم إجراؤها على الاقترانات إلى جانب العمليات البسيطة من الطرح والجمع والضرب والقسمة، وسوف نزودكم فيما يأتي بمثال بسيط على جمع الاقترانات: [6]

مثال: g(x) =2x⁵ + x³ -8x² + 6 ، f(x) = 2x² +6x+ 6 ، جد g(x) + f(x):
g(x) + f(x) = 2x⁵ + x³ -8x² + 2x²+ 6x+6
g(x) + f(x) = 2x⁵ + x³ -6x² + 6x+6

تركيب الدوال

يمكن أن نجري عملية تركيب اقترانين ق و هـ إذا كان مدى ق مجموعة جزئية من مجال هـ ونعبر عن ذلك بالصورة: (هـ ο ق) (س) ويساوي أيضًا: هـ (ق (س))، وتقرأ ه

مثال على تركيب الدوال: g(x) =4x -3 ، f(x) = 2x +1 ، جد (g ο f) (x) و (g ο f) (2)
أولًا: f ( g (x)) = f(4x-3)
f ( g (x)) = 2*(4x-3) +1
f ( g (x)) = 8 * x – 6 + 1
f ( g (x)) = 8x – 5

ثانيًا: f ( g (2))
f ( g (2)) = 8*2 – 5
16 – 5= f ( g (2))
11 = f ( g (2))

الدالة العكسية

تعد الدالة العكسية واحدة من أنواع الدوال؛ وهي عبارة عن علاقة تمثل معكوس الاقتران الأصلي، ويرمز له لمعكوس الاقتران f(x) بالرمز f^-1(x)، ويمكن أن نتأكد فيما إذا كان معكوس الاقتران اقترانًا أيضًا أو لا، من خلال التأكد من أن كل عنصر في المجال يرتبط بعنصر واحد في المدى في f(x) نفسه، ففي هذه الحالة يكون الاقتران اقتران واحد لواحد؛ وذلك من خلال التأكد من عناصر المجال وعناصر المدى أو من خلال طريقة أخرى تسمى اختبار الخط الأفقي؛ وهي تمثل برسم خط أفقي والتأكد من أنه لا يقطع منحنى الاقتران في أكثر من نقطة واحدة.

وفي هذه الحالة يكون مجال الاقتران f(x) هو مدى الاقتران f^-1(x)، ومدى الاقتران f(x) هو مجال الاقتران f^-1(x). وسوف نبين لكم طريقة استخراج الاقتران العكسي من خلال المثال الآتي:

مثال: f(x) = 4(x-5) ويكون الحل من خلال الخطوات الآتية:

• نكتب الاقتران بصورة f(x) = y
  فيصبح لدينا الاقتران بالصورة الآتية: y = 4(x-5)
• نجعل x موضوعًا للقانون من خلال الخطوات الآتية:
  الاقتران الأصلي: y = 4(x-5)
  نضرب 4 بفرعي القوس فيصبح لدينا: y = 4x-20
  من خلال إضافة 20 إلى جانبي المعادلة: y+20= 4x
  نقسم طرفي المعادلة على الرقم 4 فيصبح لدينا: y+20)/4= x)
• نبدل x ب y، ونبدل y ب x في صيغة المعادلة التي توصلنا إليها فتصبح بالشكل الآتي:
  x+20)/4= y)
• نضع f^-1(x) مكان الرمز y فتصبح بالشكل الآتي:
  x+20)/4=f^-1(x) )

شاهد أيضًا: بحث عن الكيمياء الكهربائية كامل

الدوال الرئيسة الام والتحويلات الهندسية

التحويلات الهندسية التي يمكن إجراؤها على الدوال متعددة وهي تتمثل بمجموعة من العمليات الأساسية التي تغير من موقع الرسم البياني للاقتران؛ وذلك من خلال إضافة رقم إلى الاقتران أو طرح رقم، أو ضرب الاقتران برقم معين، أو عكس الاقتران مثلًا من خلال ضربه برقم سالب. كما يمكن إيجاد العملية التي تم إجراؤها على الاقتران من خلال الرسم الأساسي والرسم الآخر بعد إجراء التحويل. والصورة الآتية تبين التحويلات الهندسية الأساسية على الاقترانات:  [7]

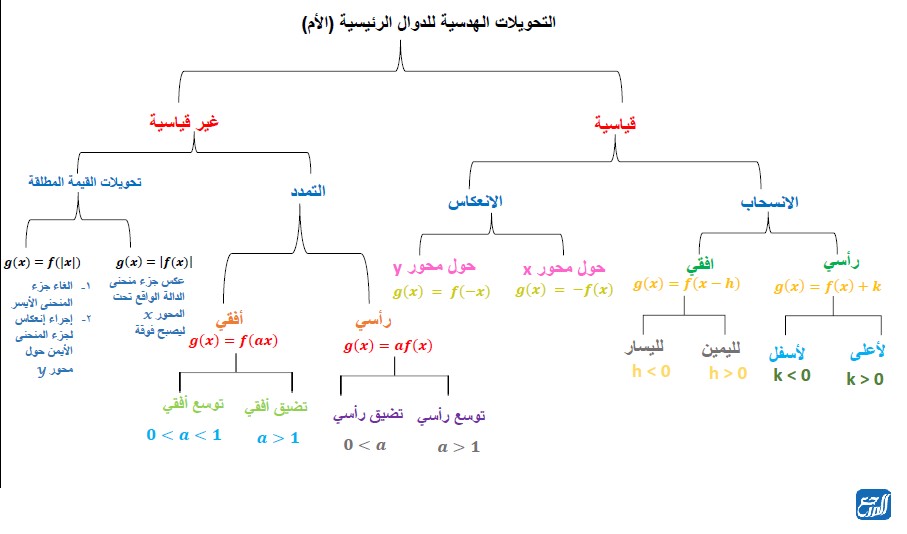
خاتمة بحث عن الدوال

في ختام هذا البحث الذي تناولت فيه الحديث عن الدوال بتعريفها وأنواعها المختلفة، وأمثلة عليها بالإضافة إلى توضيح هذه الاقترانات من خلال الرسم والتحليل، وإجراء العمليات عليها، نكون قد توصلنا إلى مجموعة من الاستنتاجات الآتية:

• تتعلق الدالة بالمدخلات المتمثلة في x والمخرجات المتمثلة في f(x).
• القيم التي يتم تعويضها في الاقترانات تسمى المجال.
• جميع المخرجات (القيم الفعلية الخارجة عن تطبيق العلاقة على قيم المجال) تسمى معًا المدى.
• الدوال هي نوع خاص من العلاقات حيث:
  • يرتبط فيها كل عنصر في المجال بعنصر واحد في المدى.
  • يُطلق على كل قيمة في المجال مع ما يقابلها في المدى زوجًا مرتبًا.
  • من خلال تعيين النقاط على المستوى الديكارتي والتوصيل بينها نتوصل إلى رسم الاقتران.
• يستفاد من الاقترانات في العديد من المجالات العلمية الفيزيائية والكيميائية والرياضية، ومجالات العلوم الحياتية المختلفة.

بحث عن الدوال وانواعها pdf

بعد إعداد البحث لا بد من حفظه بطريقة تضمن تنسيقه بشكل جيد، وهذه الطريقة هي حفظه بصيغة pdf بحيث يمكن فتحه من خلال برنامج الأدوبي ريدر عبر أي جهاز يدعمه، وبما أن بحثنا هذا عن الدوال لا بد من أن يكون البحث شامل وكامل لكل ما يخص الدوال من التعريف والأنواع وطرق التعامل معها والعمليات التي يمكن أن يتم إجراؤها عليها، وكيفية رسمها وتمثيلها على المستوى الديكارتي، وتحليلها من خلال معرفة أصفار الاقتران. ويمكنكم “من هنا” تحميل بحث عن الدوال وانواعها pdf.

بحث عن الدوال doc

يعد برنامج الوورد أفضل برنامج لكتابة الأبحاث لما يتيحه من إمكانية الكتابة والتعديل الدائمة، وإضافة الصور وتنسيق الأرقام وإضافة الرسومات البيانية لا سيما في أبحاث الرياضية مثل هذا البحث الذي تكتبه عن الدوال. فمن المعروف أن الدوال مليئة بالرموز والأرقام والمتغيرات والأسس المكتوبة إلى الأعلى وإلى الأسفل وهذه كلها تحتاج إلى برنامج يتيح هذه الخاصة. كما يمكنك من خلال اختيار أمر (معادلة) من قائمة إدراج أن تكتب المعادلة التي تحتاجها بالشكل الرياضي الواضح، تمامًا كما يلزم. ويمكنكم تحميل بحث عن الدوال “من هنا” ويمكنكم فتحه عبر برنامج الوورد بصيغة doc.

وفي نهاية هذا المقال، نكون قد زودناكم بمعلومات شاملة تلزم لكتابة بحث عن الدوال وأنواعها كامل يمكن الاستعانة بها، بالإضافة إلى نماذج بحوث مكتوبة يمكنكم تحميلها وفتحها عبر برنامج الوورد بصيغة doc، أو برنامج الأدوبي ريدر بصيغة pdf.