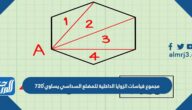
كم مستقيماً يقسم الشكل الى قسمين متماثلين تماماً

كم مستقيماً يقسم الشكل الى قسمين متماثلين تماماً متساويين في الشكل والمساحة؟ سؤال إجابته تتطلب معرفة ماهية الشكُل الهندسي وخصائصه ومعرفة شكل المُتسقيم وما يمتازُ به من خصائص هندسية ورياضية، وذلك ما سنتناوله عبر موقع المرجع مع معرفة كم مُستقيم يُقسم الشكل الهندسي لشكلين مُتماثلين.

كم مستقيماً يقسم الشكل الى قسمين متماثلين تماماً

الشكلُ الهندسي هو الشكل المُكون من عدة خطوط قد تكون مستقيمة وقد تكون مُنحنية ويُعرف رياضيًا بأنه هو النقاط المُتتالية التي تقوم بتشكيل منطقة مُغلقة عند جمعها ببعضها البعض عن طريق خطوط مُستقيمة أو منحنية، ومن ضمن أهم خصائص الأشكال الهندسية هو احتوائها على محاور تماثل يختلفُ عددها باختلاف الشكل ونوعه، تلك المحاور عبارة عن خطوط هندسية الواحد منها يُقسم الشكل الهندسي لجزئين مُتماثلين ومتساويين تمامًا، وبناءً على ما يوفره محور التماثل للشكل الهندسي من انقسام مُتماثل لأجزائه نجد أن إجابة سؤال: كم مستقيم يُقسم الشكل إلى قسمين مُتماثلين تمامًا، هي:[1]

• مستقيم واحد فقط.

شاهد أيضًا: باستعمال النموذج أدناه فإن 35 ٪ من 120 تساوي 42

أنواع الأشكال الهندسية

الأشكال الهندسية كثيرة ومُتنوعة وتختلف باختلاف الخصائص والتكوين فعلى سبيل المثال يوجد أشكال هندسية تتكون من قطع مستقيمة فقط وأشكال أخرى يدخل في تركيبها خطوط مُنحنية، وتنقسم الأشكال الهندسية تبعًا للشكل كالآتي:[1]

• أشكال تتكون من قطع مستقيمة: مثل: “الشكل الرباعي – مضلع قابل للإنشاء – مضلع دائري – عشاري – ثنائي عشري – مضلع متساوي الأضلاع – نضلع متساوي الزوايا – أحادي عشري – سداسي عشري – صليب معقوف – ثماني منتظم أو مثمن – نجمة دون خطوط متقاطعة – مضلع نجمي – نجمة عشارية”.
• أشكال تتكون من خطوط منحنية: مثل: “أربيلوس – دائرتي أرخميدس التوأم – دائرة محيطة – دائرة داخلية – دائرة النقاط التسعة – جزء دائري – قطع ناقص – رمز اللانهاية – مضلع رولو – مثلث رولو – نصف دائرة – تريكوترا – ين يان”.
• أشكال تتكون من خطوط منحنية غير دائرية: مثل: “حلزون أرخميدس- ديلتويد – قطع ناقص – قطع ناقص فائق – توماهوك”.

شاهد أيضًا: إذا كانت نسبة الماء في البطيخ ٩٢ ٪ ، فإن الكسرالعشري الذي يمثل هذه النسبة المئوية هو

محيط الأشكال الهندسية الشائع استخدامها

يتخطى عدد الأشكال الهندسية آلاف الأشكال التي تختلف باختلاف الشكل والخصائص وغير ذلك الكثير، وتتمثل القوانين الخاصة بمحيط الشائع منها فيما يلي من سطور:

• متوازي الأضلاع: مُحيط متوازي الأضلاع يُمكن الوصول إليه بكل سهولة عن طريق جمع أطوال أي ضلعين مُتقاطعين “الأكبر والأصغر” وضرب مجموعهم في اثنين.
• المثلّث وشبه المنحرف: يُمكن حساب محيط المُثلث أو شبه المُنحرف عن طريق جمع أطوال أضلع كلاهما.
• المربّع: محيط المربع سهل الاستنتاج لأن أضلعه متساوية وذلك يكون عن طريق ضرب طول الضلع في ٤.
• الدائرة: محيط الدائر يتمثل في ضرب نصف طول قطرها في باي.

شاهد أيضًا: ما مجموعة حل المتباينة ن-٣ ⩽١٢

بهذا نكون قد توصلنا لنهاية مقال كم مستقيماً يقسم الشكل الى قسمين متماثلين تماماً الذي من خلاله تبين لنا أن المُستقيمات المُقسمة الشكل الهندسي إلى قسمين متساويين تمامًا لا تتخطى المُتسقيم الواحد كما تناولنا أنواع الاشكال الهندسية تبعًا لما تتكون منه من خطوط ومحيط الشائع منها.