إذا كان المستقيمان p وq متوازيان فإن الزاويتين 3,6 متطابقتان

إذا كان المستقيمان p وq متوازيان فإن الزاويتين 3,6 متطابقتان، في علم الهندسة الرياضية المستقيم هو عبارة عن مجموعة من عدد لا متناهي من النقاط، يمتد إلى ما لا نهاية من كلا الاتجاهين، ومن خلال هذا المقال على موقع المرجع؛ سنتعرف إلى مفهوم المستقيمين المتوازيين، كما سنلقي الضوء على أنواع الزوايا الناتجة من تقاطع مستقيم لمتوازيين، وكذلك سنناقش العبارة السابقة.

المستقيمان المتوازيان

هما مستقيمان متباعدان بمقياس ثابت ولا يشتركان في نقطة، وبالتالي فهما لا يتقاطعان أبدا في أي نقطة على طول المستوى، ومن الممكن أن يكونا في المستوى نفسه، أو يكونان في مستويين مختلفين، أما المستقيمان اللذان يتقاطعان في نقطة؛ فهما مستقيمان متعامدان.

إذا كان المستقيمان p وq متوازيان فإن الزاويتين 3,6 متطابقتان

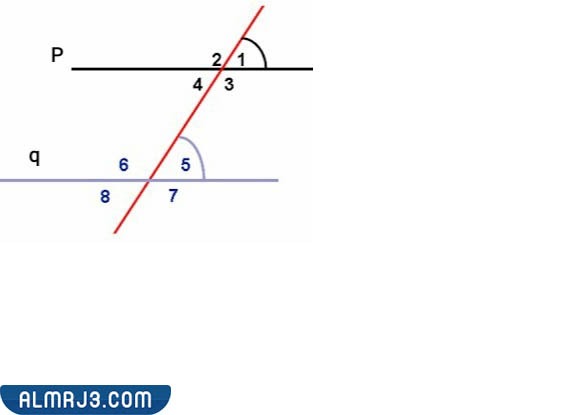
في الهندسة؛ إذا كان هناك مستقيمان متوازيان يقعان في المستوى نفسه، ثم كان لهما مستقيم قاطع؛ فإنه يتقاطع معهما في نقطتين، مكونا 8 زوايا، 4 زوايا خارجية، و4 زوايا داخلية، ولكل زاوية منها خواص تتفق أو تختلف مع غيرها من الزوايا. وبالنظر إلى العبارة السابقة؛ فإننا نستنتج أن:[1]

• العبارة صحيحة، لأنهما زاويتان متبادلتان لهما نفس القياس.

شاهد أيضًا: ماذا يسمى الخطان اللذان لا يلتقيان ابدا

العلاقة بين أزواج الزوايا الناتجة عن التقاطع

بالنظر إلى الزوايا الناتجة من تقاطع مستقيم لمستقيمين متوازيين ينتج:

•  الزوايا الداخلية: وهي عبارة عن الزوايا: 3,4,5,6.
• الزوايا الخارجية: تكون في الخارج، الزوايا: 1,2,7,8.
• الزاويتان المتحالفتان: داخليتان واقعتان في جهة واحدة، الزوايا 4 و5, 3 و6.
• الزوايا المتبادلة داخليا: تكونان في جهتين مختلفتين، الزوايا: 3 و5, 4 و6.
• الزاويتان المتبادلتان خارجيا: تكونان في جهتين مختلفتين، الزوايا: 1 و7, 2 و8.
• الزاويتان المتناظرتان: تكونان في جهة واحدة من القاطع وفي الجهة نفسها من المستقيمين، الزوايا: 1 و5, 2 و6 3 و7, 4 و8.

إلى هنا نصل لنهاية هذا المقال الذي تناول عبارة؛ إذا كان المستقيمان p وq متوازيان فإن الزاويتين 3,6 متطابقتان، كما سلطنا الضوء على العلاقة بين أزواج الزوايا الناتجة عن التقاطع.