حل نظام من معادلتين خطيتين بالتعويض
–تاريخ النشر:
جدول المحتويات
حل نظام من معادلتين خطيتين بالتعويض، يتم بهذه الطريقة حل معادلتين لهما نفس المجموعة من المتغيرات، وإعطاء قيمة عددية لكل المتغيرات؛ بحيث تتحقق جميع المعادلات، وعبر موقع المرجع سنذكر مثال على طريقة حل معادلتين خطيتين، كما ستتم الإجابة عن السؤال المطروح.
حل نظام من معادلتين خطيتين بالتعويض
لحل نظام من المعادلات الخطية باستخدام التعويض؛ نستخدم الطريقة الآتية:[1]
- نقوم بترتيب واحدة من المعادلتين بحيث يكون أحد المجهولين هو المتغير التابع.
- يتم التعويض بذلك في المعادلة الأخرى.
- يتم حل المعادلة الخطية الناتجة في مجهول واحد.
- يتم التعويض بقيمة هذا المجهول في إحدى المعادلتين.
- حل المعادلة لإيجاد قيمة المجهول الآخر.
- التحقق من صحة الحل، بالتعويض بقيمة المتغيرات في المعادلتين، حتى تتحقق صحتهما.
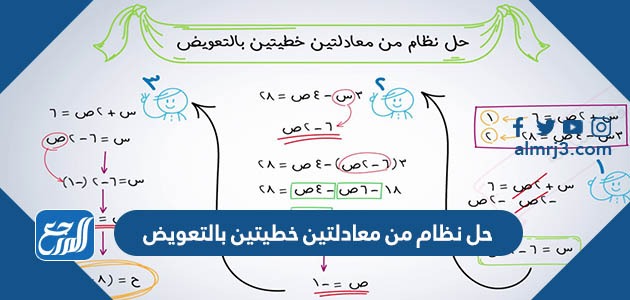
طريقة حل نظام مكون من معادلتين خطيتين باستخدام التعويض بالخطوات
هذا يعني أننا نبحث عن قيم للمتغيرات لتحقيق صحة المعادلة في النظام، وهذا مثال على ذلك:
- س + ص = 3
- س – ص = -1
- سيتم إعادة ترتيب إحدى المعادلتين لنجعل أحد المتغيرين هو المتغير التابع: ص= 3 – س.
- التعويض بالمعادلة السابقة في المعادلة الأخرى، لنحصل على: س – ص= -1 ← س – (3 – ص) = -1.
- فك القوس بالضرب في الإشارة السالبة: س – 3 + س=-1.
- بجمع السينات: 2 س – 3 = -1
- نقل -3 إلى الطرف الآخر مع تغيير الإشارة: 2 س = -1 + 3 (عددان مختلفان في الإشارة؛ نطرحهم ونضع إشارة الأكبر) إذن: 2 س = 2.
- بقسمة الطرفين على 2 فتصبح: س = 1
- نعوض بقيمة س=1 في المعادلة الأولى فتُصبح: 1 + ص = 3، وبالتالي عند نقل 1 إلى الطرف الآخر وتغيير إشارته تُصبح: ص=2
- نعوض بقيمة س، ص، 1، 2 في المعادلتين، ونتأكد من صحة الحل.
- بالتعويض في المعادلة الأولى: س+ص=3⇐ 1+2=3 (الطرف الأيمن مساوي للطرف الأيسر).
- بالتعويض في المعادلة الثانية: س -ص= -1⇐ 1 – 2= -1 (الطرف الأيمن مساوي للطرف الأيسر).
وبهذا نصل لنهاية هذا المقال، والذي تم من خلاله توضيح خطوات حل نظام من معادلتين خطيتين بالتعويض، كما تم ذكر مثال للتوضيح وبالخطوات.




















