مساحة الجزء المظلل تساوي
مساحة الجزء المظلل تساوي، تتعدد الأشكال الهندسية في الطبيعة، فهناك المربع والمستطيل والدائرة والمعين ومتوازي الأضلاع، ولكل من هذه الأشكال خصائصها التي تمتاز بها، وتُعرف من خلالها، ولكل شكل من الأشكال الهندسية قانون خاص به يتم حساب مساحته عبره، وفي هذا المقال عبر موقع المرجع سيتم الحديث عن مفهوم المساحة والأشكال الهندسية التي تتواجد من حولنا.
مفهوم المساحة
تُعرف المساحة بأنها عبارة عن قياس المنطقة المحصورة في مكان معين على سطح، أو تعرف على أنها تلك المنطقة المحصورة بين مجموعة الخطوط لتشكيل شكل هندسي معين.[1]
شاهد أيضًا: عالم رياضيات يوناني عرف بابو الهندسة من 6 حروف
مساحة الجزء المظلل تساوي
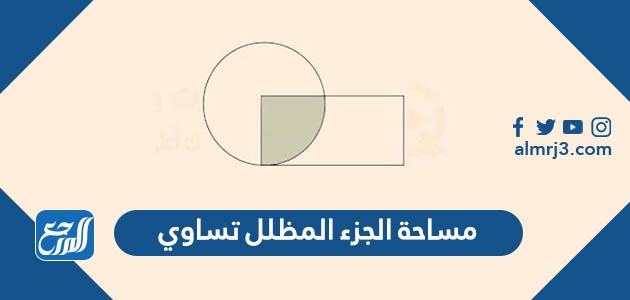
تعرفنا على مفهوم المساحة، وفي الشكل المقابل الذي يتطلب إيجاد مساحة الشكل المظلل، نقوم بحساب مساحة المستطيل أولاً والتي هي عبارة عن الطول × العرض، أي 5×2= 10، ثم نقوم بحساب مساحة نصف الدائرة، أي (1/2) × (2)^2 × ط والتي تساوي 6.28، وبالتالي فإن الإجابة على هذا السؤال هي:
- مساحة المستطيل ناقص مساحة الدائرة وتساوي 3.72
شاهد أيضًا: ما هي الهندسة الاجتماعية وما أنواعها وأساليبها
قوانين مساحات الأشكال الهندسية
لكل شكل هندسي قانون خاص به، يتم حساب مساحتها من خلالها، وفيما يلي نُورد القوانين الخاصة بحساب مساحة الأشكال الهندسية، وهي كما يلي:
- المخروط: وهو ذلك الشكل الهندسي الذي يتألف من دائرة ومستطيل مبروم، وبذلك تكون المساحة الكليّة لسطح المخروط= π × نصف قطر قاعدة المخروط × طول المائل.
- المكعب: ويتألف المكعب من ستة أوجه مربعة الشكل، وبذلك تكون مساحة سطح المكعب= 6 × مربع طول الضلع.
- متوازي المستطيلات: ويتكون متوازي المستطيلات من ستة أوجه من المستطيلات ليست جميعها متساوية، لذا فإن مساحة متوازي المستطيلات الكلية = 2×(الطول×العرض)+ 2×(الطول×الارتفاع)+ 2×(العرض×الارتفاع)= 2×(الطول×العرض + الطول×الارتفاع + العرض×الارتفاع).
- المنشور: وأوجه المنشور غير متساوية، وبالتالي فإن مساحة المنشور = 2 ×مساحة القاعدة + محيط القاعدة × الارتفاع.
- مساحة الكرة: ليس للكرة أضلاع، وبذلك فإن قانون حساب مساحة سطح الكرة = 4×π× مربع نصف القطر وبالرموز يكون، مساحة سطح الكرة = 4×π×نق² أو مساحة سطح الكرة = π×ق².
- متوازي الأضلاع: وقانونه هو: مساحة مُتوازي الأضلاع= طول القاعدة× الارتفاع.
- المربع: ويكون أطوال متساوية، حيث إن مساحة المُربّع = طول ضلع المربع².
- المستطيل: وتكون أضلاعه غير متساوية، وبالتالي فإن مساحة المُستطيل= الطول × العرض.
- المعين: حيث إنّ مساحة المعين = ½(طول القطر الأول × طول القطر الثاني) = طول الضلع × الارتفاع.
- شبه المنحرف: حيث إن مساحة شِبه المُنحرف = ½(طول القاعدة الأولى+طول القاعدة الثانية).
- الدائرة: وهي عبارة عن شكل دائري يتم حستب مساحته من طول القطر، وبالتالي فإن مساحة الدائرة= π×نصف القطر².
- المثلث: حيث إن مساحة المثلث = ½×طول القاعدة×الارتفاع.
- الهرم: حيث إن مساحة سطح الهرم= (مساحة القاعدة) + ½× (محيط القاعدة)×(الارتفاع الجانبي أو طول المائل).
- الأسطوانة: إذ أنها عبارة عن دائرتين ومستطيل مبروم لتكوين جسمها، وبالتالي فإن مساحة الأسطوانة= 2×(π×نق²)+2×π×نق×ع.
شاهد أيضًا: من مجالات الهندسة من ٩ حروف كلمة السر
وإلى هنا نكون قد وصلنا إلى نهاية مقالنا بعد أن أجبنا على السؤال، مساحة الجزء المظلل تساوي، بعد أن تعرفنا على مفهوم المساحة وكيفية حساب مساحات الأشكال الهندسية، وفق قوانينها الخاصّة.
المراجع
- wikiwand.com , مساحة , 13/12/2021




















