اي الاشكال التاليه لها تماثل دوراني حول نقطه

اي الاشكال التاليه لها تماثل دوراني حول نقطه؟ تدرس الرّياضيّات محاور التماثل للأشكال الهندسيّة، والتماثل الدوراني حول نقطة ما في الرسم البياني، حيثُ أنّها مهمة جداً في العديد من المجالات، كمجال الإنشاءات، وأعمال البناء، والتصنيع. ومن خلال موقع المرجع، سنورد في السطور التالية من هذا المقال، حل السؤال السّابق، والمقصود بالتماثُل الدوراني، بالإضافة إلى معادلة محور التماثل.

ما المقصود بالتماثل الدوراني

إنّ التماثل الدوراني عبارة عن بقاء الجسم أو الشكل كما هو عند تدويره عدّة دورات، حيث يمتلك محاور للتماثل تختلف حسب عدد دورات الجسم، ومحور التماثل يعرف بأنه عبارة عن خط مستقيم تلتف حوله البلّورة، ويوجد أكثر من نوع لمحور التماثل بحسب عدد الدورات التي يدور حول مركز البلورة، وهي كما يلي:[1]

• ثنائي التماثل.
• ثلاثي التماثل.
• رباعي التماثل.
• سداسي التماثل.

شاهد أيضًا: عدد محاور التناظر في الشكل المجاور

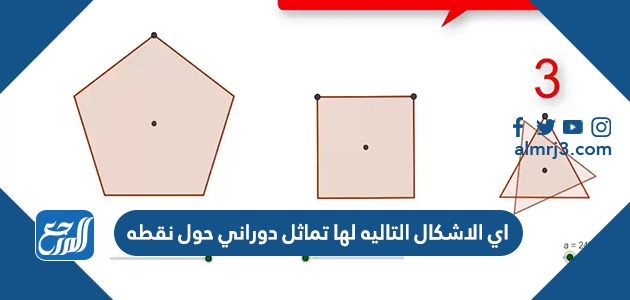
اي الاشكال التاليه لها تماثل دوراني حول نقطه

أحياناً يكون للشكل الهندسي أكثر من تماثل أو تناظر دوراني، وذلك وفقاً لعدد دورات محور التماثل حول المركز، حيثُ أنه يدور عدّة دورات حول الجسم أو الشكل الهندسي مروراً بمركز البلّورة، وفيما يلي حل السؤال حول الشكل الذي يمتلك تماثلاً دورانيّاً:

• الإجابة الصحيحة هي: المحور الرباعي، لوجود أربع أضلاع متساوية.

شاهد أيضًا: يمثل الشكل أدناه متوازي الأضلاع أ ب ج د

ما هي معادلة محور التماثل

في الرياضيّات يتم التعبير عن الخط المُستقيم الذي يقسم الرسم البياني إلى جزأين متساويين، من خلال المعادلة: س= -ب/2*أ، إذ يمثل الرمز (ب) المعامل س، والرمز (أ) المعامل س^2 في معادلة ص= س^2+ب*س+ج، أمّا في المعادلة ص= -2س^2+4س-3، فإنّ س= -4/-2*2=1، والتي تدل على معادلة محور التماثل، بحيثُ س=1، في حال موازاة محور التماثل لمحور الصادات، وقطعه محور السينات عند نقطة (1، -1).

وإلى هنا، نكون قد وصلنا إلى ختام مقالنا الذي يحمل عنوان، اي الاشكال التاليه لها تماثل دوراني حول نقطه؟ إذ أوردنا حل السؤال السابق، وتعريف التماثل الدوراني، بالإضافة إلى معادلة محور الدوران.