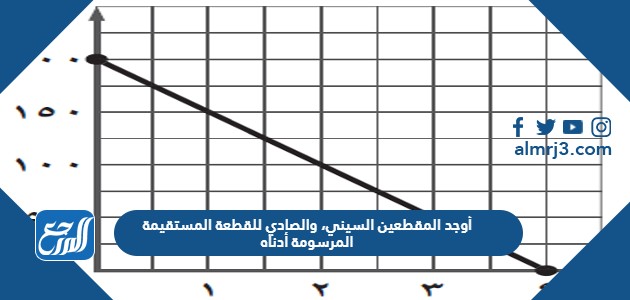
أوجد المقطعين السيني، والصادي للقطعة المستقيمة المرسومة أدناه

أوجد المقطعين السيني، والصادي للقطعة المستقيمة المرسومة أدناه، فالقطعة المستقيمة أو الخطِ المستقيم هو عبارة عن شكل هندسي مستقيمُ ممتد في جميع الاتجاهات الى المالانهاية، وليس به أي انحناءات أو سمك، وله بُعدٌ واحد فقط، ومن خلال موقع المرجع سنتعرفُ على معادلةِ الخط المستقيم، وكيفية ايجاد المقطع السيني والصادي لها.

الصيغة العامة لمعادلة الخط المستقيم

تنصُّ معادلة الخط المستقيم على أنّ أيُّ نقطة واقعة على الخط المستقيم إحداثياتها ( س،ص ) تُحقق معادلته، والتي تمثلُ عن طريقِ الآتي:[1]

• أس+ب ص+جـ = 0

حيثُ أنّ:

• أ : عدد حقيقي لا يساوي صفر.
• ب :  عدد حقيقي لا يساوي صفر.
• جـ : عدد حقيقي.

كما يوجدُ عدّة أشكال لمعادلة الخط المُستقيم، ومنّها تمثيل المُعادلة عن طريقِ العلاقة ما بين الميل والإحداثي الصادي، كالآتي:

• ص = أس + ب

حيثُ أنّ :

• أ : ميل الخط المستقيم
• ب : نقطة تقاطع الخط المستقيم مع المحور الصادي
• ص : عدد ثابت، وهو بُعد الخط المستقيم عن محورِ السينات
• س : عدد ثابت، وهو بُعد الخط المستقيم عن محورِ الصادات

شاهد أيضًا: النقاط في الجدول أدناه تقع على خط مستقيم ، ميله يساوي

أوجد المقطعين السيني، والصادي للقطعة المستقيمة المرسومة أدناه

القطعةُ المستقيمة تكونُ جزءًا من الخط المستقيم، وتُحدد بنقطتي البدايةِ والنهاية، بحيثُ يكونُ احداثي النقطتين (س1، ص1) (س2 ، ص2 )، فما هُما المقطعين السيني والصادي للقطعة المستقيمة المرسومة أدناه ؟

• المقطع السيني = 4 ، المقطع الصادي = 200

يمكنُ ايجاد الإحداثي السيني والصادي من خلالِ الشكل المُعطى، أو من خلال معادلة الخط المستقيم المُناسبة للحل.

شاهد أيضًا: ميل الخط الرأسي يكون

أشكال معادلة الخط المستقيم

إضافةً الى المعادلة الرئيسية للخط المستقيم، فإنّه يوجدُ عدّة أشكال أخرى، ومنّها:

• معادلة الخط المستقيم المار بنقطة الأصل : احداثيات نقطة الأصل (0 ، 0) وعند مرور الخط المستقيم بها فإنّ المعادلة ص = أس + ب تُصبح :
  • ص = م س ( حيثُ أنّ قيمة ب = 0 )
• معادلة الخط المستقيم الموازي لمحور الصادات : وهو الخط المستقيم الذي يوازي محور الصادات، بحيثُ يكون عموديًا على محور السينات، ومتقاطعًا معه ، ومعادلته هي:
  • س = أ  ( حيثُ أن أ هي النقطة التي يقطع عندها المستقيم محور السينات )
• معادلة الخط المستقيم الموازي لمحور السينات : وهو الخط الذي يوازي محور السينات، بحيثُ يكونُ عموديًا على محور الصادات، ومتقاطعًا معه، ومعادلته هي:
  • ص = ب ( حيثُ أن ب هي النقطة التي يقطع عندها المستقيم محور الصادات )
• معادلة الخط المستقيم التي تمثل العلاقة بين الميل والاحداثي الصادي : وتمثلُ من خلالِ المعادلة الآتية:
  • ص = م س + ب ، حيثُ أنّ
  • م : ميل الخط المستقيم ( يُساوي ظل الزاوية المحصورة بين الخط المستقيم ومحور السينات المُوجب )
  • ب : نقطة تقاطع الخط المستقيم مع محور الصادات

شاهد أيضًا: قطعتان مستقيمتان طولاهما ١٤٣ سم، ١٣١ سم، فما مجموع طوليهما؟

كيفية كتابة معادلة الخط المستقيم

يمكنُ كتابة معادلة الخط المستقيم بعدةِ طرق منّها:[2]

• كتابة معادلة الخط المستقيم عند معرفة نقطتين واقعتين عليّه : على فرض أنّ (س1 ، ص1) (س2 ، ص2) نقطتين واقعتين على الخط المستقيم، فإنّ معادلة الخط المستقيم تكونُ:
  • ( ص- ص1)/(س- س1) = (ص2 – ص1)/(س2 – س1)
• كتابة معادلة الخط المستقيم عند معرفة ميله ونقطة واقعة عليّه : على فرض أنّ م هو ميل الخط المستقيم، (س1 ، ص1) (س2 ، ص2) نقطتين واقعتين على الخط المستقيم، فإنّ معادلة الخط المستقيم تكونُ:
  • (ص- ص1) = م(س- س1)
• كتابة معادلة الخط المستقيم عند معرفة ميله ونقطة تقاطعه مع محور الصادات : على فرض أنّ ب هي النقطة التي يتقاطع فيها المستقيم مع المحور الصادي، فإنّ معادلة الخط المستقيم تكونُ :
  • ص = أس+ب
• كتابة معادلة الخط المسقيم عند معرفة نقاط تقاطعه : على فرض أنّ ل هو المقطع السيني أي قيمة س عندما ص = 0، ع هو المقطع الصادي أي قيمة ص عندما س = 0 ، فإنّ معادلة الخط المستقيم تكون :
  • س/ ل + ص/ ع = 1

الى هُنا نكون قد وصلنا الى نهايةِ مقالنا أوجد المقطعين السيني، والصادي للقطعة المستقيمة المرسومة أدناه، حيثُ سلطنا الضوء على أشكالِ معادلة الخط المستقيم، وكيفيةِ كتابتها وفقًا للمعطياتِ والصيغ المُختلفة.