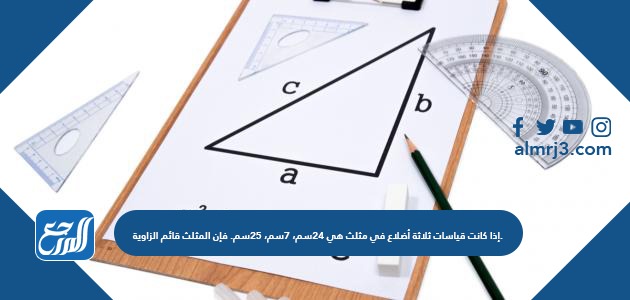
إذا كانت قياسات ثلاثة أضلاع في مثلث هي ٢٤سم، ٧سم، ٢٥سم. فإن المثلث قائم الزاوية.
جدول المحتويات
إذا كانت قياسات ثلاثة أضلاع في مثلث هي ٢٤سم، ٧سم، ٢٥سم. فإن المثلث قائم الزاوية، علم الهندسةِ أحد فروع علم الرياضيات، تهتم بدراسة الأشكال وقياس الحجوم والمساحات، مثلَ المثلث والمربع والدائرة والمستطيل وغيّرها، وايجاد كُلاً من المساحة والحجم لتلكَ الأشكال، ومن خلالِ موقع المرجع سنخصص الحديث عن نظرية فيثاغورس، والمثلث قائم الزاوية.
نص قانون المثلث قائم الزاوية
يُعرّف المثلث قائم الزاوية (Right Angled Triangle) بأنّه مثلث إحدى زواياه قائمة، بحيثُ يكونُ قياسها يساوي 90 درجة، وتحصرُ ما بين قاعدة المثلث وضلعُ القائمة، ويتبقى الضلعُ الثالث الذي يشكلُ الوتر، ويكونُ مجموع قياس الزاويتين المُتبقيتين يُساوي 90 درجة، فمنْ المعلوم بأنّ مجموع قياس زوايا المثلث يساوي 180 درجة، ويُمثل المثلث قائم الزاوية باستخدام نظرية فيثاغورس، والتي تنصُّ على أنّ مجموع مربعي الضلع الأول والثاني في المثلث قائم الزاوية يُساوي مربع الوتر:[1]
- (الوتر)2 = (الضلع الأول)2 + (الضلع الثاني)2
شاهد أيضًا: تمثل كل مجموعة من الأعداد التالية أطوال أضلاع مثلث
إذا كانت قياسات ثلاثة أضلاع في مثلث هي ٢٤سم، ٧سم، ٢٥سم. فإن المثلث قائم الزاوية
عند حلِ سؤال إذا كانت قياسات ثلاثة أضلاع في مثلث هي ٢٤سم، ٧سم، ٢٥سم. فإن المثلث قائم الزاوية، فإنّ الخطوةَ الأولى هي تطبيق الحل على قانونِ نظرية فيثاغورس، كالآتي:
- (الوتر)2 = (الضلع الأول)2 + (الضلع الثاني)2
- (25)2 = (7)2 + (24)2
- 625 = 49 + 576
- إجابة صحيحة، نظرًا لأنّ مجموع مربعي ضلعين المربع يُساوي مربع الوتر.
شاهد أيضًا: ما محيط مثلث قائم الزاوية طول وتره ١٥ سم، وطول إحدى ساقيه ٩ سم؟
أمثلة على قانون المثلث قائم الزاوية
من الأمثلة التوضيحية على قانون المثلث قائم الزاوية ما يأتي:
- المثالُ الأول: اذا كانت قياسات ثلاث أضلاع في المثلث هي 5 سم، 6 سم ، 3 سم، فإنّ المثلث قائم الزاوية ؟
- الخطوة الأولى في تحديد إنْ كان المثلث قائم الزاوية أو لا هي بتطبيقِ نظرية فيثاغورس.
- (الوتر)2 = (الضلع الأول)2 + (الضلع الثاني)2
- (6)2 = (5)2 + (3)2
- 25 + 9 = 34
- الحل: المثلث ليس قائم الزاوية، نظرًا لأنّ مربع الوتر لا يساوي مجموع مربعي ضلعي المثلث.
- المثالُ الثاني: أثبت أن المثلث الذي أطوال أضلاعه 4 سم، 3 سم، 5 سم قائم الزاوية ؟
- لإثبات أنّ المثلث قائم الزاوية فإنّ مجموع مربعي الضلع الأول والثاني في المثلث قائم الزاوية يُساوي مربع الوتر.
- تطبيق القانون: (الوتر)2 = (الضلع الأول)2 + (الضلع الثاني)2
- (5)2 = (3)2 + (4)2
- 25 = 9 + 16
- الحل: المثلث قائم الزاوية، نظرًا لأنّ مجموع مربعي الضلعين ( 4سم، 3سم) يساوي مربع الوتر (5سم).
- المثالُ الثالث: إذا كان الوتر في مثلث قائم الزاوية يساوي 25 سم، والقاعدة فيه تساوي 15 سم، أوجد طول الضلع الآخر؟
- الخطوة الأولى: تطبيق قانون نظرية فيثاغورس
- (الوتر)2 = (الضلع الأول)2 + (الضلع الثاني)2
- (25)2 = (15)2 + (الضلع الثاني)2
- 625 = 225 + (الضلع الثاني)2
- 625 – 225 = (الضلع الثاني)2
- 400 = (الضلع الثاني)2
- الحل: أخذ الجذر للطرفين : الضلع الثاني = 20 سم.
- المثالُ الرابع: إذا كان طول ضلعي مثلث قائم الزاوية يساوي 9 سم، 8 سم على التوالي، فإنّ طول الوتر؟
- عند ايجاد طول الوتر في المثلث قائم الزاوية يجبُّ تطبيق القانون وأخذ الجذر له.
- (الوتر)2 = (الضلع الأول)2 + (الضلع الثاني)2
- (الوتر)2 = (9)2 + (8)2
- 81 + 64 = 145
- الوتر = √145 = 12.4 سم
شاهد أيضًا: مساحة مثلث يبلغ ارتفاعه 3 سم وطول قاعدته 4 سم يساوي
الى هُنا نكون قد وصلنا الى نهايةِ مقالنا إذا كانت قياسات ثلاثة أضلاع في مثلث هي ٢٤سم، ٧سم، ٢٥سم. فإن المثلث قائم الزاوية، حيثُ سلطنا الضوء على تعريفِ المثلث قائم الزاوية، ونظرية فيثاغورس.
المراجع
- byjus.com , Right Angled Triangle , 07/10/2021





















