خريطة مفاهيم النهايات والاشتقاق

خريطة مفاهيم النهايات والاشتقاق، علمُ التفاضلِ والتكامل هو أحدُ فروع علم الرياضيات يتعاملُ مع إيجادِ المِشتقات والتكاملات للاقترانات وخصائِصها، بطرقٍ ترتكز على جمع نواتج طرح لا نهائية، والتفاضل هو معدّل تغيّر الاقتران عند أحدِ المُتغيّراتِ فيه، أما التكاملُ فهوَ عملية عكسية للتفاضل، ومن خلالِ موقع المرجع سنتعرفُ على خريطة مفاهيم النهايات والاشتقاق التي تندرجُ تحت مصطلح التكامل والتفاضل.

خريطة مفاهيم النهايات والاشتقاق

خريطةُ المفاهيمِ هيّ تخطيط رسوميّ يكونُ له بعدين، يشملُ على مفاهيم مُتخصصة ومُتعلقة ببعضها البعض، حيثُ أنّ القاعدّةُ العلوية من الهرم تشمل على مفاهيم شاملّة وعامة أكثر، فيما أنّ القاعدة السفليّة تشمل على مفاهيم مُتخصصة وأقلّ شموليّة، وترتبط المفاهيم جميعها من خلالِ قاعدة معروفة، وتمثيلُ خريطة مفاهيم النهايات والاشتقاق مُدرجةٌ بالصورة الآتيّة:

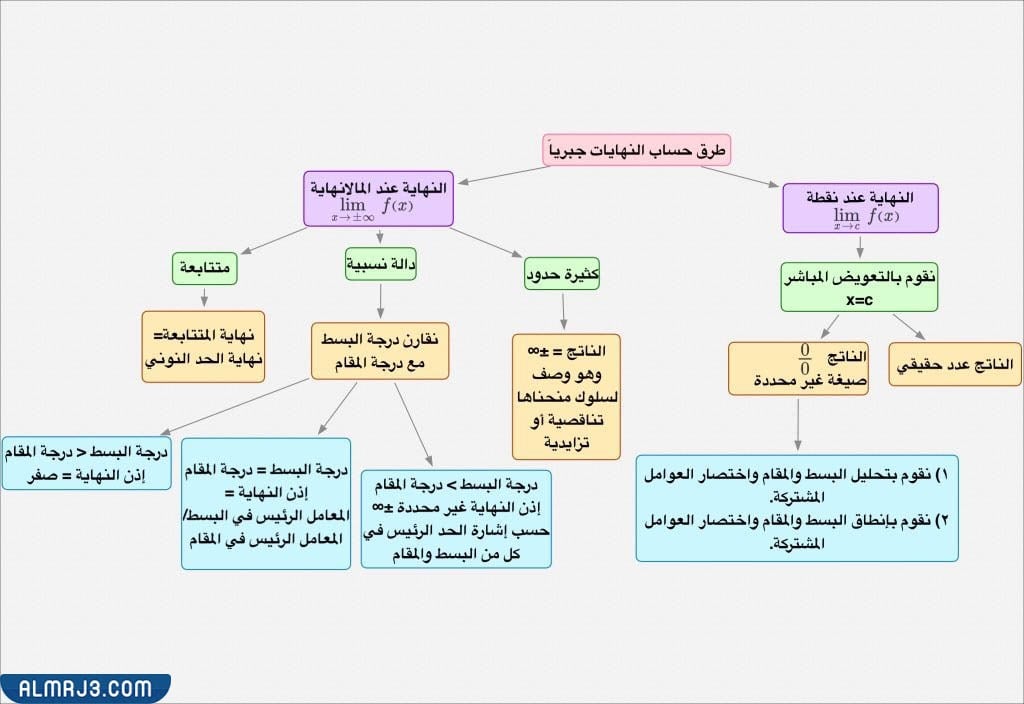
وعامةً فإنّه عند حساب النهايات يجبّ أولاً تعويض قيمة أ التي تقترب منها س في الاقتران، ليمثل الناتج قيمة النهاية، وفي حالِ كانت النتيجة قيمة غيرُ معرفة فإنّه يتمٌّ اللجوء إلى عدّة طرق حسبْ نوع الدالة منْ طريقةُ التعويض، وطريقة التحليل إلى عوامل، وطريقة الضرب بالمرافق، وطريقة توحيد المقامات، وقانون لوبيتال.

شاهد أيضًا: باستعمال النموذج أدناه فإن 35 ٪ من 120 تساوي 42

طرق حساب النهايات جبريًا

أوضحت الخارطة المفاهيميّة للنهايات والاشتقاق طُرق حساب النهايات جبريًا، والتي تُقسّم إلى تحديدِ المسألة إنْ كانت النهايّة عند نقطة، أم كانت النهايةّ عند المالانهايّة على النحوِ الآتّي:

• النهايّة عند نقطة: فإنّ الحلُ اختصارًا هوَ بالتعويض المُباشر، والناتجُ إما عدد حقيقيّ أو صيغة غيرُ محددة، ولحلِ الصيغةُ غير المحددة فإنّه يتمُّ تحليل البسط والمقام، وايجاد العوامل المُشتركة.
• النهاية عند المالانهايّة: يختلفُ إيجاد النهايات إن كانت النهاية عند المالانهايّة حسبْ الآتّي:
  • إنْ كانت الدالة كثيرة حدود، فإنّ الناتج موجب أو سالب مالانهايّة، وهو وصف لسلوكِ مُنحناها بشكل تناقصيّ أو تزايديّ.
  • إن كانت دالة نسبيّة، فإنّه يجب مُقارنة درجةُ البسط مع درجة المقام، فإنْ كانت درجةُ البسطة أكبر من درجة المقام، تكون النهاية غير محددة، حسبْ إشارة الحد الرئيسي في كل من البسط والمقام، وإن كانت درجةُ البسطِ أصغرُ من درجة المقام، فإنّ النهاية صفر، وإن كانت درجة البسط تساوي درجة المقام فالنهايةُ هي حاصلُ قسمة المامل الرئيسي في البسط على المعامل الرئيسي في المقام.
  • نهاية المتتابعة = نهاية الحد النوني.

شاهد أيضًا: لتكمل الرسم بأداة رسم المنحنيات عليك إقفال الرسم بالوصول إلى نقطة البداية .

خصائص النهايات

تستخدمُ النهايات في الرياضيات لإيجاد القيمة الناتجة عن اقتراب قيمة س للاقتران ق(س) من قيمة معينة أخرى، وهناك العديد من الخصائص المتعلقة بالنهايات، وهي كالآتي:[1]

• نها_س←أ س = أ، أي أن نهاية الاقتران ق(س)=س، وذلك عندما تقترب قيمة س من القيمة أ تساوي القيمة أ.
• نهاية الاقتران المرفوع لأس ما، تساوي ناتج رفع نهاية الاقتران لنفس الأس: أي أنّ:
  • نها_س←أ (ق(س))^ن = (نها _س←أ ق(س))^ن.
• تتوزع النهاية على عملية الضرب، أي أنّ:
  • نها_س←أ ق(س)×ع(س) = نها _س←أ ق(س)×نها_س←أ ع(س).
• تتوزع النهاي على عملية القسمة، أي أنّ:
  • نها_س←أ ق(س)/ع(س) = نها _س←أ ق(س)/نها_س←أ ع(س)، بشرط أن لا تكون نها _س←أ ع(س) تساوي صفر.
• ناتج ضرب الثابت في نهاية الاقتران يساوي ناتج نهاية الثابت مضروبًا بالاقتران، أي أنّ:
  • نها_س←أ جـ×ق(س) = جـ×نها_س←أ ق (س)؛ حيث جـ عدد ثابت.
• نهاية الثابت تساوي الثابت نفسه، أي أنّ:
  • نها_س←أ جـ = جـ، حيث جـ عدد ثابت.
• نهاية مجموع اقترانين معاً، تساوي مجموع نهاية كل منهما لوحده، أي أنّ:
  • نها_س←أ (ق(س)+ع(س)) = نها_س←أ ق(س)+نها_س←أ ع(س).

شاهد أيضًا: أي مما يأتي تبين الصورة القياسية لكثيرة الحدود

إلى هُنا نكونُ قد وصلنا إلى نهاية مقالنا خريطة مفاهيم النهايات والاشتقاق، حيثُ سلطنا الضوءَ على كيفيّة حساب النهايات جبريًا، وخصائص النهايات جميعُها.