ما هو قانون محيط المستطيل ومساحته

ما هو قانون محيط المستطيل ومساحته فالأشكال الهندسية من أكثر الأشياء التي نشاهدها في حياتنا اليومية مثل المباني والمنازل والأراضي التي نزرعها أو الحدائق التي نجلس بها وما إلى ذلك، وعلمياً يتم تعريف الأشكال الهندسية على أنها عبارة عن مساحة مغلقة بواسطة حد ما يتم إنشاؤه من خلال الجمع بين كمية محددة من المنحنيات أو الخطوط المستقيمة والنقاط، فمثلاً المربع يتشكل من الخطوط المستقيمة حيث أن هذه الخطوط تسمى الضلوع بينما الدائرة تتشكل من الخطوط الغير مستقيمة وتسمى المنحنيات وكذلك الأمر بالنسبة للمستطيل الذي يشبه المربع، وفي مقالنا اليوم عبر موقع المرجع سنتعرف على المستطيل وقانون حساب محيطه ومساحته وحساب قطره وطول ضلعه إضافة إلى ذكر كل ما يخص هذا الموضوع. 

المستطيل

هو عبارة عن شكل هندسي يتكون من أربعة جوانب تحدد شكله تسمى الضلوع ولها عدة خصائص وهي:[1]

• كل ضلعين متقابلين متوازيين و متساويين في الطول.
• على عكس المربع الذي أضلاعه متساوية فإن الضلعين المتوازيين في المستطيل غير متساويين بالطول مع الضلعين الآخرين المتوازيين والأطول بينهما يسمى الطول بينما الأصغر يسمى العرض.
• مثل المربع تماماً جميع زوايا المستطيل قائمة والزاوية هي التي تتشكل بين الضلعين المتجاورين وهما الطول والعرض.
• قطري المستطيل متساويين بالطول ومتقاطعين في المنتصف.

شاهد أيضًا:ما هو قانون مساحة المثلث

ما الفرق بين المساحة والمحيط 

بالرغم من أن المساحة والمحيط خاصيتان مهمتان للأشكال ثنائية الأبعاد في علم الرياضيات إلى أنهما مختلفان من حيث الوظيفة وهي:[1]

• المحيط: يحدد المحيط مسافة حدود الشكل الهندسي ثنائي الأبعاد.
• المساحة: تحد موضع المنطقة أو الحيز من الفراغ الذي يشغله الشكل الهندسي ثنائي الأبعاد.

قانون محيط المستطيل

كما تعرفنا سابقاً المحيط هو مسافة حدود الشكل ويتم حساب محيط المستطيل بجمع أطوال أضلاعه الأربع، وبما أن كل ضلعين متوازيين متساويين بالطول وهما ضلعي الطول وضلعي العرض فيكون قانون محيط المستطيل الشكل التالي:[1]

• محيط المستطيل = (الطول ×2) + (العرض ×2)

كما يمكن أن يعبر عنها بصيغة أخرى صحيحة أيضاً وهي:

• محيط المستطيل = (الطول +العرض) × 2

مثال على حساب محيط المستطيل 

يريد مزارع أن يحيط الحقل المستطيل الشكل الذي يملكه بسياج من الأسلاك الشائكة لمنع دخول الغرباء إلى حقله أو الحيوانات التي تدمر المزروعات فيه، فكم يحتاج من السياج ليحيط الحقل إذا كان طوله 50 متراً وعرضه 25 متراً؟[2]

الحل: لحساب طول السياج المطلوب علينا أن نعرف محيط الحقل، وبما أن الأرض مستطيلة الشكل ونعلم الطول والعرض نقوم بتطبيق قانون حساب محيط المستطيل، فيكون الحل وفق التالي:

• محيط الحقل = (طول الحقل×2) + (عرض الحقل×2)
• محيط الحقل = (50×2)+(25×2)
• محيط الحقل = 150 متر.

قانون مساحة المستطيل 

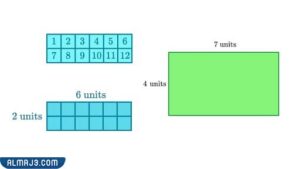
مساحة المستطيل تعبر عن الحيز من الفراغ الذي يشغله هذا الشكل الهندسي وتعبر عن عدد الوحدات أو القطع التي تشكله، وكمثال توضيحي للتعريف إذا كان لدينا مستطيل مساحته 12 متر مربع فهذا يعني أن هناك 12 قطعة على شكل مربع تشكله، ويتم حساب مساحته من حاصل ضرب الطول ضرب العرض وفق الشكل التالي:[2]

• مساحة المستطيل = الطول × العرض

مثال على حساب مساحة المستطيل

في المسألة التالية لدينا مزرعة مستطيلة الشكل يبلغ طولها 80 متراً وعرضها 60 متر فكم تبلغ مساحة هذه المزرعة؟[2]

الحل: نقوم بتطبيق قانون مساحة المستطيل الذي ينص على أن المساحة = الطول × العرض وبالتالي يكون الحل:

• مساحة المزرعة = 80×60
• مساحة المزرعة = 4800 م²

شاهد أيضًا: تم ترتيب ١٠٠ مقعد في حفل مسرحي على شكل مربع . ماعدد المقاعد في كل صف

حساب قطر المستطيل

المستطيل له قطران متساويان في الطول ومتقاطعان في المنتصف وكل قطر منهما يقسم المستطيل إلى مثلثين قائمين متساويين في المساحة والمحيط، وبما أن الطول والعرض معلومين في المثلث القائم الذي يشكله قطر المستطيل داخل المستطيل يتم حساب القطر باستخدام نظرية فيثاغورس التي تقول أن مربع طول الوتر يساوي مربع طول الضلعين القائمتين، وبالتالي يكون قانون حساب قطر المستطيل هو:[3]

• (مربع طول المستطيل) + (مربع عرض المستطيل) = (مربع طول القطر)

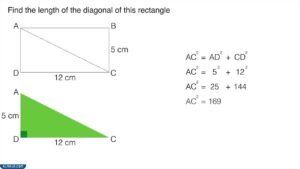
مساحة المستطيل بمعلومية طول قطره

يمكن حساب مساحة المستطيل بمعلومية طول قطره باستخدام نظرية فيثاغورس دون معرفة أطوال أضلاعه الحقيقية، ويتم ذلك عن طريق استنتاج مساحة المثلثين القائمين الذين يشكلهما القطر وفق العملية التالية:[3]

• نستخدم نظرية فيثاغورس لحساب طول الضلعين والتي تنص على أن مربع طول الضلعين القائمتين تساوي مربع طول الوتر.
• بعد الحصول على طول الضلعين القائمتين يمكن حساب مساحة المستطيل بحساب مساحة المثلثين القائمين وجمع النتيجة مع بعضها.
• يمكن حساب المساحة للمستطيل بشكل أسهل بعد أن نعرف طول الضلعين القائمتين عن طريق تطبيق قانون مساحة المستطيل التي تعرفنا عليها سابقاً.

ملاحظة هامة: لا يمكن تقدير طول وعرض المستطيل بشكل دقيق عند استخدام نظرية فيثاغورث إلا إذا كان أحد الضلعين معلوم كما هو موضح بالصورة المرفقة.

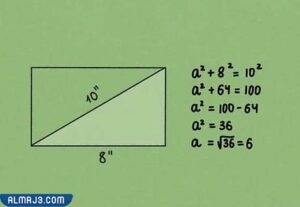
قانون طول المستطيل

يتم حساب طول (ط) أو عرض (ع) المستطيل باستخدام قانون محيط (مح) أو مساحة (مس) المستطيل وفق التالي:[3]

• بما أن (مح) = (ط×2) +( ع×2) فإن (ط×2) = (مح) – ( ع×2) وبالتالي ط = (ط×2) ÷ 2.
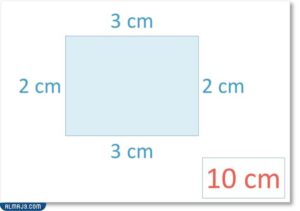
• كمثال على استنتاج الطول من المحيط إذا كان مح=10 و ع=2 فإن ط= 10-(2×2) وتساوي 6 وبالتالي ط= 6÷2=3.
• بما أن (مس) = (ط) × (ع) فإن (ط) = (مس) ÷ (ع).
• كمثال على استنتاج الطول من المساحة إذا كان مس=6 وع=2 فإن ط=6÷2 أي أن ط=3.

وبهذا القدر نصل إلى نهاية مقالنا الذي كان بعنوان ما هو قانون محيط المستطيل ومساحته والذي تعرفنا من خلاله على المستطيل وكيفية حساب محيطه ومساحته والفرق بين المساحة والمحيط مع الأمثلة التوضيحية كما تعرفنا على كيفية حساب قطره وطول ضلعه.