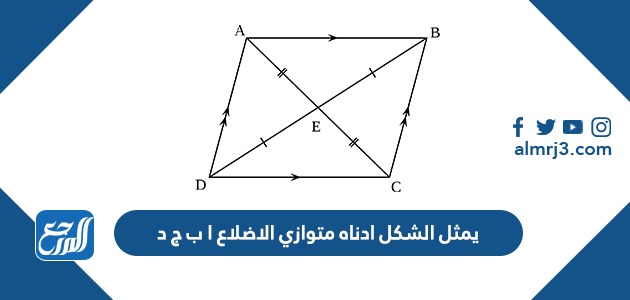
يمثل الشكل أدناه متوازي الأضلاع أ ب ج د

يمثل الشكل أدناه متوازي الأضلاع أ ب ج د

في المسألة: يمثل الشكل أدناه متوازي الأضلاع أ ب ج د، إذا مد الضلع ج د إلى النقطة هـ ، فاستنتج العلاقة بين الزاوية د أ ب والزاوية أ د ج ؟

• العلاقةُ بين الزاويتين د أب ، أ د ج هي علاقةُ تكامل.

حيثُ وجدت علاقة التكاملِ ما بين الزاويتين د أ ب ، أ د ج لاشتراكهما في نفسِ الضلع أ ب، فكلُ زاويتين متجاورتين متكاملتين، أي أن محموعُ قياسهما 180 درجة، وهذا من أحدِ خصائص متوازي الأضلاع.

قانون حساب مساحة متوازي الأضلاع

يتمُّ حساب مساحة متوازي الأضلاع بثلاث طرقٍ مُختلفة حسبَ المُعطى في المسألة الرياضية، كالآتي:[1]

حساب مساحة متوازي أضلاع باستخدام الارتفاع وطول القاعدة

يتمّ استخدامه في حال عُلمت مساحة القاعدة والارتفاع، وينصُّ على:

• مساحة متوازي الأضلاع = طول القاعدة × الارتفاع

الارتفاع هو الخط الواصل ما بين القاعدة والضلع المجاور لها، ويمكنُ حسابه من خلال القانون الآتي:

•  الارتفاع = طول الضلع الجانبي ×  جا ( الزاوية المجاورة)

ومن الأمثلة على ذلك:

• المثالُ الأول: إذا كانت طول قاعدة متوازي أضلاع 10 سم، وارتفاعه 5 سم، جد مساحته؟
  • المُعطى: طول قاعدة المتوازي = 10 سم ، ارتفاع المتوازي = 5 سم
  • الحل : مساحة متوازي الأضلاع = طول القاعدة × الارتفاع
  • م = 10 × 5 = 50

اقرأ أيضًا: مساحه شبه المنحرف الذي طول قاعدته 12.4 متر و 16.2 متر وارتفاعه 5 امتار تساوي

حساب مساحة متوازي أضلاع باستخدام ضلعي المتوازي والزاوية المحصورة

يتمُّ استخدامه في حال معرفة طول ضلعي المتوازي المتجاورين ومقدار الزاوية المحصورة بين الضلعين، وينصُ على:

• مساحة متوازي الأضلاع = الضلع الأول × الضلع الثاني × جا ( الزاوية المحصورة بين الضلعين)

ومن الأمثلة على ذلك:

• المثالُ الأول: إذا كانت أطوال أقطار متوازي أضلاع تساوي 2 سم ، 5 سم على التوالي، وكان مقدارُ الزاوية المحصورة بينهما = 60، احسب مساحة متوازي الأضلاع؟
  • المُعطي: طول ضلع المتوازي الأول = 2 سم ، طول ضلع المتوازي الثاني = 5 سم، مقدار الزاوية بينهما = 60
  • الحل: مساحة متوازي الأضلاع = الضلع الأول × الضلع الثاني × جا ( الزاوية المحصورة بين الضلعين)
  • 2 × 5 × جا ( 60) = 8.6

حساب مساحة متوازي أضلاع باستخدام قطري المتوازي والزاوية المحصورة

يتمُّ استخدامه في حال معرفة أطول قطري المتوازي الواصل بين أحد رؤوس المتوازي والرأس المقابل له، ومعرفة الزاوية المحصورة، وينص علي:

• مساحة متوازي الأضلاع = 1/2×(القطر الأول×القطر الثاني×جا (الزاوية المحصورة بين القطرين))

ومن الأمثلة على ذلك:

• المثالُ الأول: إذا كانت أطوال أقطار متوازي أضلاع تساوي 2 ، 5 سم على التوالي، وكانت الزاوية المحصورة بينهما = 60 درجة، جد مساحة متوازي الاضلاع؟
  • المعطى: طول قطري المتوازي = 2 ، 5 سم ، مقدار الزاوية المحصورة بين القطرين = 60 درجة
  • الحل: مساحة متوازي الأضلاع = 1/2×(القطر الأول×القطر الثاني×جا (الزاوية المحصورة بين القطرين))
  • 0.5 × 2 × 5 × جا 60 = 4.3

الى هُنا نكون قد وصلنا الى نهايةِ مقالنا يمثل الشكل أدناه متوازي الأضلاع أ ب ج د، حيثُ سلطنا الضوء على كيفية حساب مساحة متوازي الأضلاع بمعلومية ضلعين وزاوية بينهما، وبمعلومية القاعدة والارتفاع.