التمثيل بالقطاعات الدائرية للبيانات في الجدول أدناه هو

ما هو القطاع الدائري

يمكن تعريف القطاع الدائري بأنه جزء من الدائرة يحده نصفا قطر من الجهتين ليتكون شكل مغلق ويتم حساب مساحة القطاع الدائري بسهولة إذا كان كل من قيمة طول نصف قطر الدائرة وقياس الزاوية. وبشكلٍ عام تعتمد مساحة القطاع الدائري في أي دائرةٍ على الزاوية المركزيّة لهذا القطاع، فكلما زادت الزاوية المركزية له زادت مساحة القطاع، وكلما نقصت قلت مساحته، كما تتناسب طردياً مع طول قوس القطاع.[1]

شاهد أيضًا: إذا كان التمثيل بالقطاعات الدائرية أدناه يبين مكونات النفايات

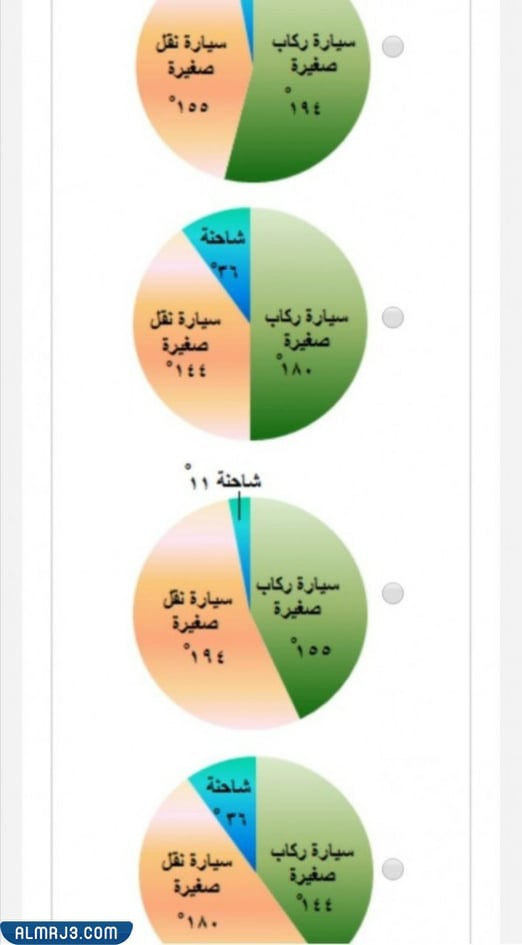
طريقة حساب مساحة القطاع الدائري

يتم التعبير عادة عن مساحة الدائرة كاملة بالقانون: π×نق²، وعندما يتطلب الأمر حساب مساحة جزء من الدائرة فإن ذلك يتم من خلال زاوية القطاع الدائري، ولأن قياس زوايا الدائرة كاملة يساوي 360 درجة، فإن نسبة زاوية القطاع الدائري إلى 360 درجة تتناسب مع مساحة الجزء من الدائرة المراد قياس مساحته. وبشكل عام تعتمد مساحة القطاع الدائري في أي دائرةٍ على الزاوية المركزيّة لهذا القطاع. فكلما زادت الزاوية المركزية له زادت مساحة القطاع، وكلما نقصت قلت مساحته.

مثال على حساب مساحة القطاع الدائري

إذا كان نصف قطر القطاع الدائري 3م، وطول القوس المقابل له 5πسم علماً أن زاويته مقاسة بالراديان، جد مساحة هذا القطاع الدائري.

الحل: باستخدام قانون طول القوس=نق×θ، ينتج أن 3θ=5π، ومنه θ=5π/3راديان باستخدام القانون مساحة القطاع الدائري= 0.5×زاوية القطاع× مربع نصف القطر=3²×0.5×5π/3، ومنه مساحة القطاع الدائري=23.55سم².