أنواع المثلثات حسب الاضلاع والزوايا
جدول المحتويات
أنواع المثلثات حسب الاضلاع والزوايا؟ المثلث هو شكل هندسي، وهو أصغر الأشكال الهندسية، إنه مضلّع مغلق، يتكوّن من ثلاثة أضلاع، بينها ثلاثة زوايا، صنّفه العلماء ضمن ستّة مجموعات، وفقاً لنوع الزوايا التي يتشكل منها هذا المثلث، أو وفقاً لأطوال أضلاعه، وللتعمق أكثر في أنواع المثلثات، ومعرفة ما الفروقات بينها، سوف يقدم لنا موقع المرجع هذا المقال لتوضيح معظم الأفكار والقوانين حول المثلثات والتي تضبط جميع القيم المتعلقة بها.
أنواع المثلثات حسب الاضلاع والزوايا
يمكننا تصنيف المثلثات إلى نوعين مختلفين، ويفيد هذا في معرفة خصائص المثلث وصفاته، وبالتالي سهولة حساب القيم المجهولة التي تتعلق به، كطول الضلع أو قياس الزاوية، لأن المثلث هو شكل هندسي مضبوط بدقة، وله خواص محددة تضبط لنا الحدود القصوى والدّنيا المسموحة لطول ضلع أو قياس زاوية، وهذه الأنواع هي: [1]
المثلث بحسب قياس زواياهِ
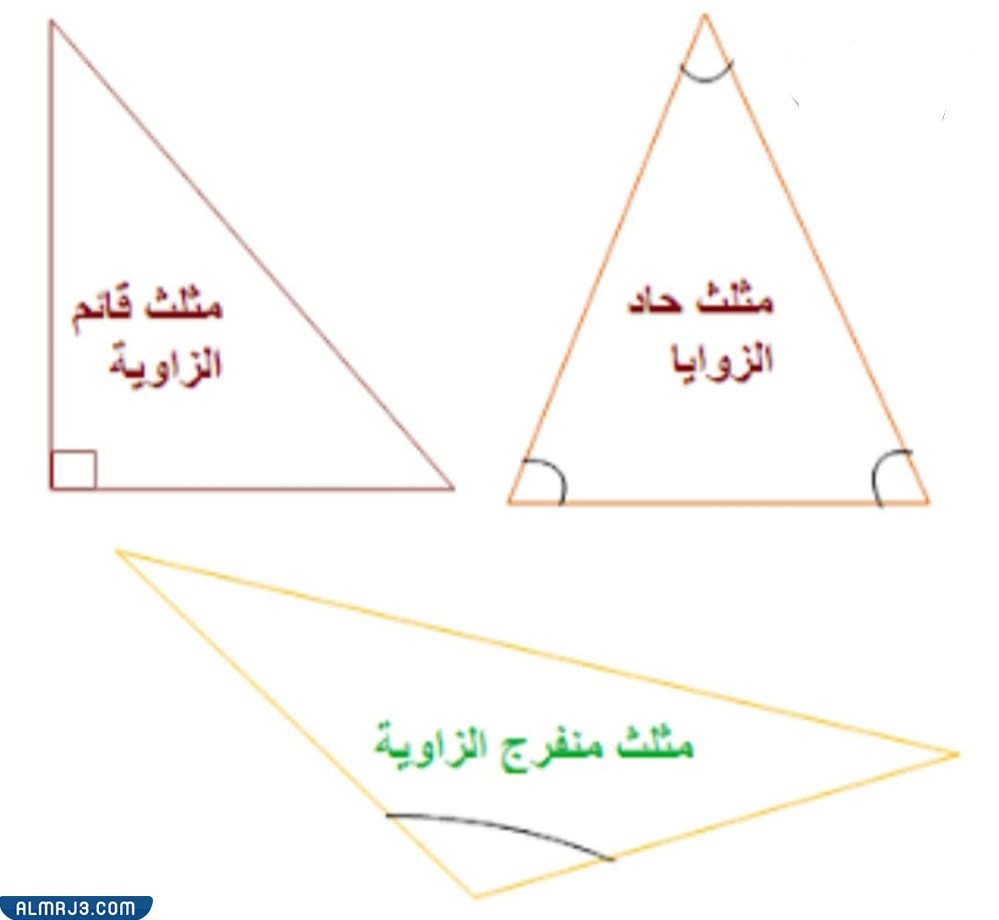
سوف نذكر الأنواع الثلاثة للمثلث بحسب قياس زواياه، وهي:
- المثلث قائم الزاوية: وهو المثلث الذي يتواجد فيه زاوية قائمة، قياسها تسعون درجة، وزاويتان حادتان.
- المثلث منفرج الزاوية: وهو المُثلث الّذي تُوجد فيه زاوية منفرجة، قياسها أكبر من تسعين درجة، وزاويتان حادتان.
- المثلث حادّ الزوايا: وهو المثلث الذي يتكون من ثلاثة زوايا حادّة قياس كلّ منها أقل من تسعون درجة.
المثلث بحسب أطوال أضلاعِهِ
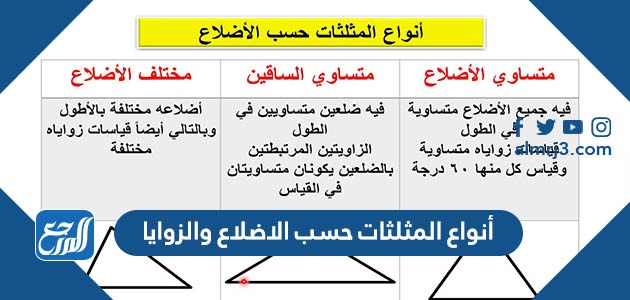
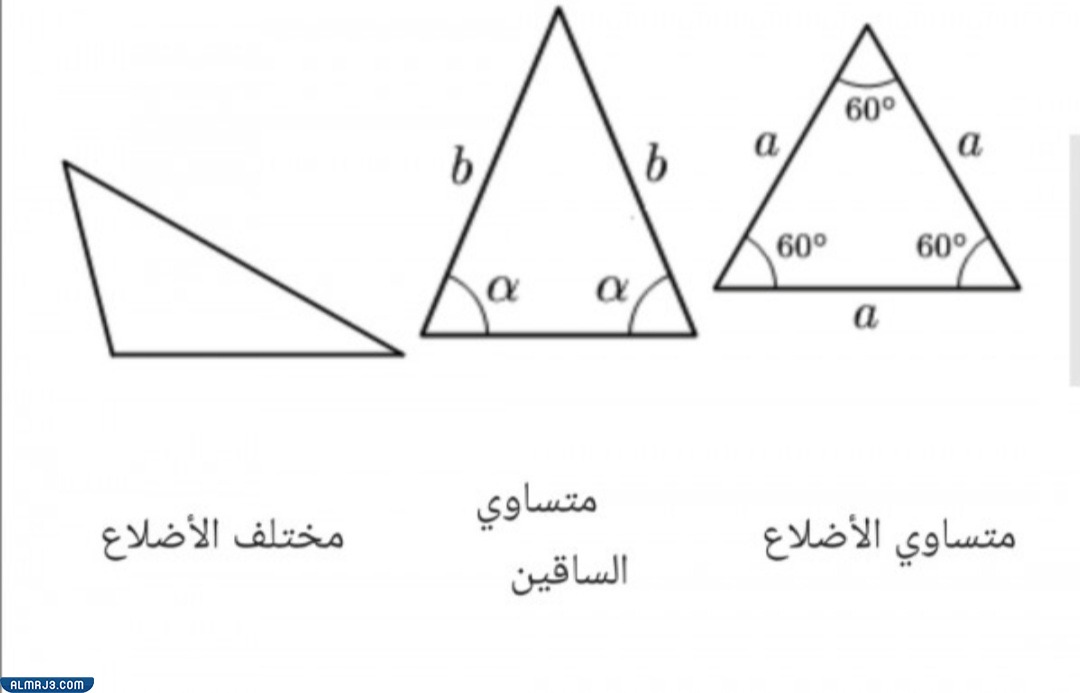
لدينا ثلاثة أنواع للمثلث بحسب أطوال أضلاعه وهي:
- المثلث المتساوي الأضلاع: وهو المثلث الذي تكون فيه جميع الأضلاع متساوية بالطول، وبذلك تكون جميع زواياه متساوية بالقياس أيضاً، وقياس كلّ منها يساوي الستون درجة.
- المثلث المتساوي الساقين: وهو المثلث الذي يكون فيه ضلعان متساويان بالطول، والضلع الثالثة مختلفة بالطول، ويحصر هذان الضلعان زاوية تسمَّى زاوية الرأس، والزاويتان الباقيتان تُسميان زاويتا القاعدة، ويكون لهما القياس ذاته.
- المثلث المختلف الأضلاع: وهو المثلث الذي يتكون من ثلاثة أضلاع أطوالها مختلفة، وبالتالي تحصر بينها ثلاثة زوايا مختلفة بالقياسات.
شاهد أيضًا: اوجد قياس كل من الزوايا المرقمه
أمثلة على أنواع المُثلّثات
حدد نوع المثلث بحسب القيم المعطاة، على حسب قياسات زواياه وأطوال أضلاعه:
| القيم المعطاة للمثلث | الجواب: نوع المثلث |
| مثلث قياس زواياه: 90, 60, 30. | يحتوي المثلث على زاوية قائمة فهو مثلث قائم الزاوية، و قياسات زواياه مختلفة، ومنه فإن أطوال أضلاعه مختلفة، فهو مختلف الأضلاع. |
| مثلث قياس زواياه: 90, 45, 45. | هو مثلث قائم الزاوية بسبب وجود زاوية قائمة وتساوي 90 درجة، وفيه زاويتان متساويتان فهو مثلث متساوي الساقين. |
| مثلث قياس زواياه: 110, 30, 40. | إن هذا المثلث هو مثلث منفرج الزاوية، لأنه يحوي زاوية منفرجة، وهو مختلف الأضلاع بما أن قياسات زواياه الثلاثة مختلفة عن بعضها. |
| مثلث أطوال أضلاعه: 6، 6، 6. | هو مثلث متساوي الأضلاع، لأن أضلاعه الثلاثة لها نفس الطول، وبالتالي جميع زواياه متساوية بالقياس، ويساوي كل منها 60 درجة. |
| مثلث فيه زاوية 120 درجة و طولا الضلعين اللذان يحصران هذه الزاوية هما 6cm و 6cm | مثلث منفرج الزاوية لأن فيه زاوية أكبر من 90 درجة، ومتساوي الساقين، لأن فيه ضلعان متساويان بالطول. |
شاهد أيضًا : يصنف المثلث الذي قياسات زواياه هي ١٠٠ درجة ، ٤٥ درجة ، ٣٥درجة الى،
نظرية فيثاغورس في المثلث
وهي إحدى العلاقات الأساسية في الهندسة الإقليدية، اكتشفها العالِم فيثاغورس، وتُطبق هذه النظرية على أضلاع المثلث القائم. [2]
نَصُّ النظريّة
يساعد هذا القانون في حساب طول ضلع مجهولة في مثلث قائم، وتنص على أنّه في كل مثلث قائم: مجموع مربعي الضلعين القائمتين، يساوي مربع طول الوتر.
مثال محلول عن نظرية فيثاغورس
لدينا abc مثلث قائم في a، طول الضلع ab=4 cm، وطول الضلع ac=3 cm، ما هو طول الضلع bc=؟، الحل: بتطبيق نظرية فيثاغورس في المثلث القائم فإن: ab²+ac²=bc² وبالتّعويض نجد أن طول الضلع bc=5cm.
عكس نظرية فيثاغورس
ومن خلال عكس نظرية فيثاغورس، يمكننا إثبات أن مثلث ما قائم، أم أنه غير قائم، وتنص على أنه إذا تساوى مجموع مربعي ضلعين في مثلث مع مربع طول الضلع الثالثة، فإن المثلث قائم في الزاوية التي تحصر هذين الضلعين.
مثال محلول عن عكس نظرية فيثاغورس
يوجد لدينا mkp مثلث فيه: طول mk=9 cm، طول pk=12 cm، طول mp=15 cm، هل mkp مثلث قائم ولماذا؟ الحل: بتطبيق نظرية فيثاغورس نجد أن mk²+pk²=mp²، ومنه فإن المثلث قائم في k وذلك بحسب عكس نظرية فيثاغورس.
شاهد أيضًا: المثلث الذي يحتوي زاوية قائمة يعتبر
تطابق المثلثات
يُقصد بتطابق المثلثات، هو أن جميع قياسات زوايا المثلث الأول وجميع أطوال أضلاعه، تساوي ما يقابلها من المثلث الآخر، من حيث قياسات الزوايا وأطوال الأضلاع، وهناك عدة حالات يُمكن فيها تأكيد أن مثلثين مختلفين، متطابقين أم غير متطابقين، وهذه الحالات هي:
- ضلعان وزاوية: أي أن ضلعين وزاوية محصورة بينهما من المثلث الأول، تساوي بالقيم ما يقابلها من المثلث الثاني.
- زاويتان وضلع: أي أن زاويتين والضلع المحصورة بينهما، تتساوى بالقيم مع ما يقابلها من المثلث الآخر.
- ثلاثة أضلاع: أي أننا نقول عن مثلثين أنهما طبوقان، عندما تتساوى أطوال أضلاعه مع أطوال أضلاع المثلث الآخر.
- ضلع ووتر في المثلث القائم: يتطابق مثلثان قائمان، عندما يتساوى طول ضلع قائمة وطول الوتر من المثلث الأول، مع ما يقابلها من المثلث الثاني.
- ملاحظة: لا يكفي أن تتساوى جميع قياسات زوايا مثلث مع جميع قياسات زوايا مثلث آخر، حتى نقول أنهما متطابقان.
تشابه المثلثات
نقول عن مثلثين أنهما متشابهان، عندما ينتج أحدهما عن الآخر بتكبيرهِ أو بتصغيرهِ، وهناك عدة حالات لتشابه المثلثات وهي:
- التناسب في أطوال الأضلاع: أي أننا نقول عن مثلثين أنهما متشابهان، إذا كانت هناك نسبة ثابتة بين أطوال أضلاع الأول، مع أطوال أضلاع الثاني، على سبيل المثال: مثلث أبعاده 3,4,5, ومثلث آخر أبعاده 12,9,16, نلاحظ أن هناك تناسباً بين أطوال أضلاع المثلث الأول، مع أطوال أضلاع المثلث الآخر، وتنتج عنها بضربها ب 3، فإن المثلثان متشابهان.
- زاويتان: يتشابه مثلثان عندما تكون قياسات زاويتين من الأول، متساوية بالقياس مع زاويتين من المثلث الآخر.
- ضلعان متناسبان وزاوية متساوية: أي أننا نقول أن هذين المثلثين متشابهين، عندما يوجد ضلعان من الأول متناسبان مع ضلعان من الثاني، وتتساوى الزاوية المحصورة بينهما من المثلث الأول مع الزاوية المحصورة بين الضلعين من المثلث الثاني.
وبهذا القدر الشامل ينتهي مقالنا هذا، والذي تعلمنا فيه ما هي أنواع المثلثات حسب الاضلاع والزوايا، وهي ستة أنواع، مثلث قائم الزاوية، مثلث منفرج الزاوية، مثلث حاد الزوايا، مثلث متساوي الأضلاع، مثلث متساوي الساقين، مثلث مختلف الأضلاع، وعددنا بعض الأمثلة المحلولة عن أنواع المثلث بحسب المعطيات، وتطرقنا إلى الحديث عن نظرية فيثاغورس وعكسها، وتعلمنا ما معنى تطابق المثلثات وتشابه المثلثات، وما هي الحالات المختلفة لكل منها.
المراجع
- cuemath.com , Types of Triangles , 23/10/2021
- teoremadepitagoras.info , Theory of Pythagoras , 23/10/2021