بحث عن القطع المتوسطة والارتفاعات في المثلث

بحث عن القطع المتوسطة والارتفاعات في المثلث، فاْلأشكال الهندسية المختلفة، هي محور علم الهندسة وتطبيقاته، وهو العلم الذي يهتم بشكل الأشياء الفردية، والعلاقات المكانية بين الكائنات المختلفة، وخصائص الفضاء المحيط بما في ذلك الأشكال، وعلم المثلثات هو أحد موضوعات علم الهندسة، والذي يعتني بدراسة المثلثات وخصائصها باستخدام المهارات الهندسية، والقطع المتوسطة والارتفاعات في المثلث هو أحد الفروع التي يقوم علم المثلثات بدراستها، وفي مقالنا اليوم عبر موقع المرجع سوف نقدم بحث شامل عن هذا الموضوع.  

مقدمة بحث عن القطع المتوسطة والارتفاعات في المثلث

في علم الرياضيات، لطالما كانت الأشكال الهندسية معرض اهتمام كافة العلماء الرياضيين، والتي أثمرت عن نظريات قوانين واستنتاجات هامة، تحدد هذه الأشكال واستخداماتها وحساباتها المختلفة، والمثلثات هي أحد هذه الأشكال الهندسية، التي يرتبط بها العديد من النظريات والقوانين الهامة، بما في ذلك أضلاعها وزواياها والقطع المستقيمة والارتفاعات في داخلها، وهذا ما سيكون محور هذا البحث.

شاهد ايضًا: زوايا المثلثات المشهورة

بحث عن القطع المتوسطة والارتفاعات في المثلث

هناك الكثير من الحقائق التي تتعلق حول الارتفاعات والقطع المتوسطة في المثلثات، وخاصة أنه في غالبية الأحيان يتم الخلط بين هذين المصطلحين الرياضيين، ولذلك هناك الكثير من الأمور التي سوف يتم التطرق لها سياق هذا البحث، في الشرح المفصل للقطع المتوسطة والارتفاعات في المثلث، بما في ذلك تعريفها وخصائصها والفرق بينها والقوانين والنظريات التي تخُصهما وكل ما يتعلق بهما، والتي سَنبدؤها باكتساب نظرة عامة على علم المثلثات وخَصائص المثلثات ونظرياتها الثابتة، كنقطة محورية يبنى عليها هذا البحث.[1]

علم المثلثات

بشكل مختصر،علم المثلثات هو فرع من فروع الرياضيات المعني بوظائف محددة لـ الزوايا وتطبيقها على الحسابات، والذي يجد تطبيقات ضخمة في مجالات متنوعة، ويتعامل هذا الفرع بشكل أساسي مع دراسة العلاقة بين أضلاع وزوايا المثلث، ويساعد في العثور على الزوايا أو الجوانب المفقودة أو غير المعروفة للمثلث باستخدام الصيغ المثلثية أو الوظائف أو الهويات المثلثية، ويتم تصنيف علم المثلثات إلى فرعين مختلفين، وهما علم المثلثات المُستوي، الذي يتعامل مع المثلثات المستوية ثنائية الأبعاد وكل ما يرتبط بها، وعلم المثلثات الكروية، والذي يتعامل مع المثلثات ثلاثية الأبعاد وكل ما يرتبط بها.[1]

خصائص ونظريات ثابتة في هندسة المثلثات المستوية

بما أن المثلثات هي المضلعات التي لها ثلاثة جوانب وثلاث زوايا، يتم تحديد نظريات المثلث أساسًا بناءً على زواياها وجوانبها، والتي تعتبر أساسيات علم الهندسة، فيما يخص هذا الشكل الهندسي، ومن أهم هذه النظريات الثابتة حول المثلثات:[1]

• مجموع الزوايا الداخلية الثلاث للمثلث يساوي 180 درجة.
• زوايا قاعدة المثلث متساوي الساقين متطابقة، كما أن الزوايا المقابلة لجوانب متساوية في مثلث متساوي الساقين متساوية في القياس أيضًا.
• قياس الزاوية الخارجية للمثلث يساوي مجموع الزوايا الداخلية المقابلة.
• في مثلث قائم الزاوية، يكون مربع طول الوتر مساويًا لمجموع مربعات الضلعين الآخرين، وهذه تسمى نظرية فيثاغورس.
• مجموع ضلعي هذا الشكل الهندسي، أكبر من مجموع ضلعه الثالث.
• مساحة حاصل ضرب ارتفاع المثلث وقاعدته، يساوي ضعف مساحته.
• عندما يكون لثلاثة أضلاع لمثلثين نفس القيمة، أو أنها متناسبة مع بعضها البعض، فإنها تكون متطابقة.
• عندما يكون ضلعان من مثلثين متناسبين، والزاوية بينهما متشابهة، فإن هذين المثلثين سيكونان متشابهين.
• الضلع المقابل لأكبر زاوية في المثلث هو الضلع الأكبر.

القطعة المتوسطة في المثلث

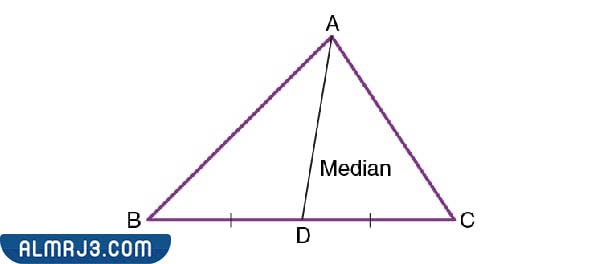
القطعة المتوسطة في المثلث، هو عبارة عن قطعة مستقيمة يتم رسمها من رأس المثلث إلى النقطة الوسطى في الضلع المقابل، ويقسم بذلك الجانب الآخر من المثلث إلى جزأين متساويين، وهذا يعني أننا نعلم أن هذه القطعة هي بالفعل قطعة متوسطة، وذلك من خلال حصولنا على هذه الأجزاء المستقيمة المتساوية التي يتكون منها المثلثات المقسومة.[2]

خصائص القطعة المتوسطة

والتي تتمثل فيما يلي:[2]

• يمكن أن يكون لدينا ما يصل إلى ثلاثة متوسطات، وهي واحد من كل رأس إلى منتصف الضلع المقابل. 
• عندما نرسم ثلاثة وسطاء في المثلث، فإنهم يلتقون دائمًا في نقطة واحدة. وتعرف هذه النقطة المفردة باسم Centroid للمثلث.
• المتوسطات تقسم المثلثات إلى قسمين، ويتشكل المثلثان الجديدان عن طريق إضافة وسيط لهما ليشكل مساحات متساوية.
• من خلال المتوسطات الثلاثة للمثلث، سوف يتشكل ستة مثلثات مكونة من مناطق متساوية.

نقطة التقاء القطع الوسيطة ومركز الثقل

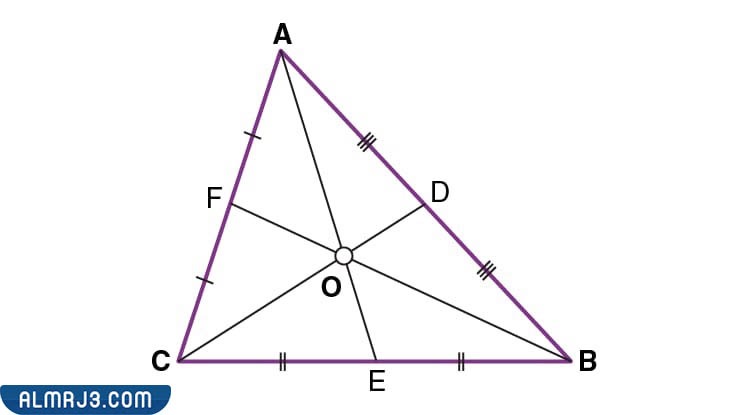
عند تقاطع المتوسطات، تسمى النقطة المشتركة بين المتوسطات الثلاثة بالنقطة الوسطى أو Centroid أو نقطة التزامن، وسكون دائمًا داخل المثلث على عكس نقاط التزامن الأخرى مثل المركز العمودي، واجتماع الوسطاء في النقطة الوسطى عرض خاصية غريبة، فدائمًا ما يكون النقطة الوسطى هي ثلثي الطريق على طول كل وسيط من الزاوية الداخلية لذلك الوسيط، وخاصية أخرى لهذه النقطة، أنها تسمى بمركز الكتلة أو مركز ثقل المثلث، وهذه ليست مجرد نقطة نظرية، فمن خلال رسم المتوسطات الثلاثة، يمكن العثور على المكان المحدد الذي سيتوازن فيه المثلث الموجود فعليًا بشكل مثالي.[2]

قانون القطعة المتوسطة

هناك عدة قوانين ونظريات وضحت أبعاد القطعة المستقيمة والخصائص التي تمنحها، ومن هذه القوانين والنظريات:[3]

• نظرية مركز الثقل: في أي متوسط ​​لمثلث، تكون المسافة بين مركز الثقل الذي عرفناه سابقاً، ومركز جانبه المقابل في المثلث، هو  ثلث أو ⅓ من طول ذلك الوسيط، وبالمقابل، تكون النقطة الوسطى هي ⅔ أو ثلثي المسافة الممتدة من أي رأس للمثلث، إلى نقطة منتصف الضلع المقابل، ط.
• نظرية الوسيط لِأبولونيوس: هي نظرية هندسية أولية تربط طول متوسط ​​المثلث بِأطوال أضلاعه، وتنص أن مجموع مربعي ضلعين من أضلاع المثلث، يساوي مجموع نصف مربع الضلع الثالث، ومرتين من مربع الوسيط المقابل لهذا الضلع الثالث.

مثال تطبيقي على نظرية القطعة المتوسطة

السؤال: مثلث أضلاعه 7 و 6 و 10 سم. أوجد طول الوسيط في ضلع الطول 10 سم.[3]

الحل: من المصطلحات المذكورة أعلاه، أ = 10 سم، ب = 7 سم، ج = 6، ونصف الضلع المطلوب إيجاد الوسيط به هو م= أ÷2 = 10÷2 = 5 سم، وبتطبيق قانون نظرية الوسيط لِأبولونيوس، ومن خلال استبدال القيم المطلوبة، يكون الحل هو:

• ج²+ب² = 2 (م²+د²)

• 6²+7² = 2 (5²+د²)

• 49+36 = 2 (25+د²)

• 49+36 = (2×25) +د²

• 49+36 = 50+د²

• د² = (36+49) – 50

• د² = 85 – 50 = 35

• د = جذر د² = جذر 35 = 4.183 

كيفية ايجاد القطعة المتوسطة في ​​المثلث

يتم ذلك بعدة خطوات باستخدام الفرجار، وهي أدق طريقة تقريباً، فإذا كان لدينا المثلث ABC، وأردنا أن نقوم ببناء المنصف العمودي للطرفين AB و BC للحصول على نقاط المنتصف لتلك المقاطع، كما في الصورة المرفقة، فسنقوم بما يلي:[3]

• نضبط عرض الفرجار على ما يزيد قليلاً عن نصف طول AB.

• نضع رأس الفرجار في النقطة A، ونصنع قوسًا على كل جانب من جوانب AB.
• ودون تغيير عرض البوصلة، من الرأس أو النقطة B، نرسم أقواساً تتقاطع مع القوسي الأولين في النقطتين E وF، كما هو موضح في الشكل أدناه.
• ثم نرسم خطًا من E إلى F، لتتكون لدينا النقطة S، وهي النقطة التي تتقاطع فيها القطعة المستقيمة EF مع ضلع المثلث AB، وبذلك تكون النقطة S هي نقطة المنتصف للضلع AB، والمقابلة للزاوية C، فتكون القطعة المستقيمة للزاوية C هي CS.
• وبعد أن حصلنا على أول قطعة مستقيمة، نكرر العملية مع الخط BC، وننشئ النقطة T على BC، كما هو موضح في الصورة أدناه، وبذلك أصبح لدينا نقاط المنتصف لـ BC وAB التي سنربطها ببساطة.
• وكذلك الأمر بالنسبة للضلع الأخير ونقطة المنصف عليه، ثم نرسم القطع المتوسطة جميعها لنحصل على نقطة ثقل المثلث.

ارتفاع المثلث

الارتفاع هو في الأساس قطعة مستقيمة متعامدة يتم رسمها من رأس مثلث إلى الجانب المقابل، فإذا كان لدينا مثلث رأسه A، والضلع المقابلة للرأس هي BC، فيكون الارتفاع هو الضلع المرسوم بشكل عمودي من الرأس A، على الضلع المقابلة للرأس وهي BC، كما يمكننا القيام بذلك من أي رأس للمثلث على الضلع المقابلة له، لكننا نراه في أغلب الأحيان بشكل أوضح من الأعلى.[4]

خصائص ارتفاع المثلث

تختلف الارتفاعات وتتشابه مع القطعة المتوسطة في بعض الخصائص، ولكنها في ذات الوقت تميز بين الإثنين، ومن أهم خصائص الارتفاعات:[4]

• يمكن أن يحتوي كل مثلث على 3 ارتفاعات، أي ارتفاع واحد من كل رأس على الضلع المقابلة له.
• تلتقي جميع الارتفاعات الثلاثة للمثلث دائمًا في نقطة واحدة بغض النظر عن شكل المثلث.
• الارتفاع هو أقصر مسافة من الرأس إلى الجانب المقابل له.

الفرق بين متوسط ​​وارتفاع المثلث

قد يبدوان هذين المصطلحين أنهما متشابهان إلى حد ما، كما أن هناك بعض الخصائص المتشابهة بينهما، لكن فعلياً، هناك فرق جوهري بينهما، ويؤثر هذا الفرق على طريقة حساب كل منهما بشكل مختلف تماماً، ويتلخص الفرق فيما يلي:[4]

• الارتفاع هو منصف عمودي على أي جانب من المثلث، ويقيس المسافة بين الرأس والخط الذي هو الجانب المقابل.
• الوسيط هو قطعة خطية تربط الرأس بالنقطة المركزية في الجانب المقابل، أي أنه لا يجب أن يكون الوسيط متعامدًا في كل مرة. 

وبالرغم من ذلك، وفي حالة وجود مثلث متساوي الأضلاع تحديداً، يكون الوسيط والارتفاع متماثلين دائمًا.

شاهد أيضًا: أنواع المثلثات حسب الاضلاع والزوايا

خاتمة بحث عن القطع المتوسطة والارتفاعات في المثلث

يعد علم المثلثات من أهم العلوم التي تنعكس نتائجه على تطبيقات مختلفة من الأمور الحياتية، سواء من الحاجة لحساب الزوايا والمسافات في مجالات مثل علم الفلك ورسم الخرائط والمسح وإيجاد مدى المدفعية وغيرها، وخصائص ونظريات وتطبيقات القطع المتوسطة والارتفاعات في المثلث، هي جزء مهم للغاية من هذا العلم، وهذا ما تعرفنا عليه بشكل موسع في سياق هذا البحث.

بحث عن القطع المتوسطة والارتفاعات في المثلث pdf

تعد علوم الرياضيات، من أهم العلوم التطبيقية في حياة الإنسان، بما في ذلك علم المثلثات الذي يعد من أقدم العلوم التي عرفها الإنسان، وخير مثال عليها، الأهرامات الفرعونية التي يعد تصميمها جزء من هذا العلم، ونظراً لأهمية هذا البحث الذي يتكلم عن أحد أساسيات هذا العلم، نقدمه كملف pdf يمكن تحميله “من هنا“، حتى يبقى مرجع يمكن العودة إليه وقت الحاجة.

بحث عن القطع المتوسطة والارتفاعات في المثلث doc

 تتعدد استخدامات الأبحاث العلمية، كما تتعدد سبل الإستفادة منها في أي مجال من مجالات الحياة، وبسبب أهمية هذا البحث وضرورة الإستفادة منه بشتى السبل، نقدمه كملف doc يمكن تحميله “من هنا“، بحيث يمكن استخدامه كملف وورد يسهل طباعته على الورق وحفظه كملف أرشيفي مكتوب يستعان به وقت الحاجة.

وبهذا القدر نصل إلى نهاية مقالنا الذي كان بعنوان بحث عن القطع المتوسطة والارتفاعات في المثلث، والذي قدمنا من خلاله بحث شامل عن هذا الموضوع، بما في ذلك التعريفات المختلفة لهذين المصطلحين وخصائصهما والفرق بينهما والقوانين والنظريات التي تخُصهما وكل ما يتعلق بهما.