يقع مركز الدائرة الخارجية للمثلث خارج المثلث اذا كان نوع المثلث
جدول المحتويات
يقع مركز الدائرة الخارجية للمثلث خارج المثلث اذا كان نوع المثلث، تعتبر الرياضيات الهندسية مجال من مجالات الرياضيات المتعددة، وعلم المثلّثات من ضمن أحد فروع الهندسة الذي يتعلّق بوصف الزوايا المثلثيّة والجوانب الرياضية المتعلّقة بها، ويستخدم هذا الفرع في فروع الرياضيات المختلفة، ومن خلال المقال التالي على موقع المرجع سنتعرف على المثلث وأنواعه من حيث قياس أضلاعه وزواياه.
تعريف المثلث
المثلث هو شكل مغلق ثنائي الأبعاد، وثلاثي الأضلاع، ويتكوّن من ثلاث قطع مستقيمة تُشكّل الأضلاع تتقاطع في نهايتها لتكوين الرؤوس أو الزوايا، وتتم تسمية المثلث غالباً بالاعتماد على رؤوسه، وله ثلاث زوايا يكون مجموع قياسها 180 درجة، ودائماً ما يقابل أقصر ضلع من المثلث أصغر زاوية داخلية، ويقابل أطول ضلع من المثلث أكبر زاوية داخلية.
شاهد أيضًا: مركز المثلث هو نقطة تلاقي
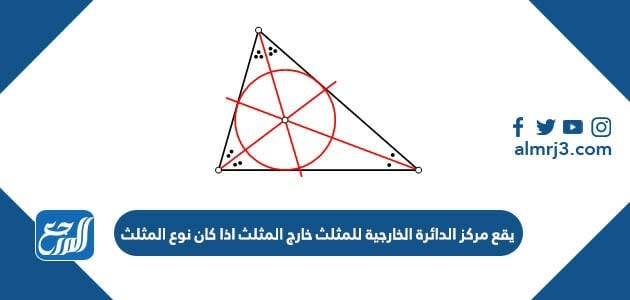
يقع مركز الدائرة الخارجية للمثلث خارج المثلث اذا كان نوع المثلث
يمكن أن يقع مركز الدائرة الخارجية للمثلث داخل المثلث أو خارجه أو على أحد أضلاعه، ويرجع ذلك إلى نوع المثلث، وعندما يقع مركز الدائرة الخارجية خارج المثلث يكون نوع المثلث:
- مثلث منفرج الزاوية.

أنواع المثلثات من حيث قياس الزوايا الداخلية
تقسم المثلثات من حيثُ قياس الزوايا الداخليّة إلى الآتّي:[1]
- المثلث حاد الزاوية: هو المثلث التي يكون قيّاس زواياه جميعَها أقل من 90 درجة، مثلاً المثلث الحاد هـ د و، تكون فيّه قِياس الزاوية هـ د وفيه يساوي 50 درجة، وقياس الزاوية د هـ ويساوي 81 درجة، وقياس الزاوية و د هـ يساوي 49 درجة.
- المُثلث منفرج الزاوية: هو المثلث الذي يكون فيّه قياس زاوية واحدة أكبر من 90 درجة، مثلاً المثلث المنفرج هـ د و، تكون فيّه قِياس الزاوية هـ د وفيه يساوي 120 درجة، وقياس الزاوية د هـ ويساوي 30 درجة، وقياس الزاوية و د هـ يساوي 30 درجة.
- المثلث قائم الزاوية: هو المثلث الذي يكون فيه قياس زاوية واحدة يساوي 90 درجة، ويكون مجموع قيّاس الزاويتين الأُخرتين 90 درجة، مثلاً المثلث قائم الزاوية هـ د و، تكون فيّه قِياس الزاوية هـ د وفيه يساوي 90 درجة، وقياس الزاوية د هـ ويساوي 50 درجة، وقياس الزاوية و د هـ يساوي 40 درجة.
شاهد أيضًا: كم عدد المثلثات المختلفة التي يمكن رسمها
أنواع المثلثاث من حيث أطوال الأضلاع
تقسم المثلثات من حيثُ أطوال الأضلاع إلى الآتّي:
- مثلث متساوي الأضلاع: هوَ المثلث الذي تتساوى فيّه جميع أطوال أضلاعه، كذلكَ تتساوى فيّه جميع قياسات زواياه.
- مُثلث مختلف الأضلاع: هو المثلث الذي تختلفُ فيه جميع قياسات أطوال أضلاعه، وكذلك قياسات زواياه.
- مثلث متساوي الساقين: هو المثلث الذي يتساوى فيه طول ضلعيّن، وبالتالي تتساوى فيّه قياس زاويتين.
المراجع
- cuemath.com , Types of Triangles , 02/02/2022






















