مركز المثلث هو نقطة تلاقي

مركز المثلث هو نقطة تلاقي، تتعددُ الأشكال الهندسيّة في علمِ الريّاضياتِ ما بينَ الهرم والمُثلث والدائرة والمعين وشبّه المُنحرف ومتوازي المُستطيلات والعديدُ غيّرها، وبطبيعةِ الحال فإنّ خصائصَ كُلَ شكل هندسيّ تختلفُ عن الآخر، كما وتختلفُ قوانينِ حسابْ المساحة والمُحيطُ أيضًا، ومن خلالِ موقع المرجع سنخصصُ الحديثَ عن المثلث وأنواعه وخواصه المُختلفة.

المثلث

يُمكنُ تعريف المثلث (بالإنجليزية: Triangle) على أنّه شكلٌ هندسيْ مُغلق مُكونْ ثلاث أضلاع، وثلاث زوايا، وثلاث رؤوس، بحيثُ تتقاطعُ الأضلاع في نهايتها لتكوين الرؤوس أو الزوايا، ويُمكن أن تكون قياسات زوايا المُثلث مُختلفة عن بعضها البعض خلافًا للمستطيل أو المربع، فهي ليست قائمة، وتتم تسمية المثلث غالبًا بالاعتماد على رؤوسه، وله ثلاث زوايا يكون مجموع قياسها 180 درجة، والزاوية الخارجية للمثلث تساوي مجموع الزاويتين الداخليّتين البعيدتين.[1]

شاهد أيضًا: اي مثلث اطوال الاضلاع المعطاه ومثلث قائم الزاويه

مركز المثلث هو نقطة تلاقي

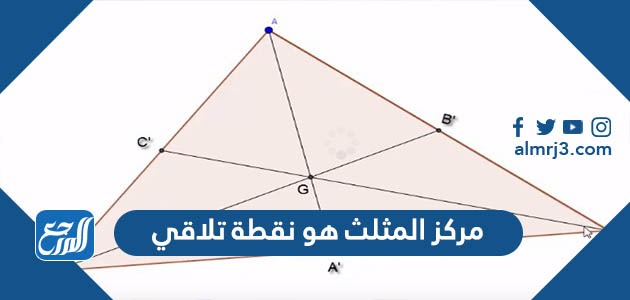
المُثلث هوَ مُضلع ثنائيَ الأبعاد وثلاثيّ الأضلاع، مُكون من ثلاثة خطوط متصلّة، ولهُ عدّةُ خصائص، كأنْ يكونُ مجموع زوايّاه 180 درجةّ، وأنْ يتشابه المثلثان إذا كانت الزوايا المتقابلة لكل من المثلثين مُتطابقة وأطوال أضلاعهما مُتناسبة، وغيّرها، وإجابةُ سؤالِ مركزُ المثلث هو نقطة تلاقي تكونُ هيّ ؟

• نقطةُ تقاطعُ مُستقيّمات خاصة للمثلث.

حيثُ يوجدُّ عدّة خصائِص وميّزات تحددُ مراكزَ المُثلث، ومنْ أهمُها النقطةُ المركزيّة أو مركزُ ثقل المثلث وهِيّ الموضع المتوسط لجميع نقاط المثلث في جميع اتجاهات الإحداثيات، ومركزُ قائم وهو نقطة التقاء جميع الارتفاعات في المثلث، ونقطةُ فيّرما أيضًا، ومركز دائرة النقاط التسع، ومركزُ الدائرة المُحاطة بالمثلث أو مركز الدائرة الداخلية المماسة للمثلث.

شاهد أيضًا: ما عدد محاور التماثل في المثلث المتطابق الاضلاع

أنواع المثلثات

تُقسم المثلثات إلى عدّة أنواع بناءً على الآتّي:

أنواع المثلثات من حيث قياس الزوايا الداخلية:

تُقسم المثلثات من حيثُ قياس الزوايا الداخليّة إلى الآتّي:

• المثلث حاد الزاوية: هو المثلث التي يكونُ قيّاس زواياه جميعَها أقلُّ من 90 درجة، مثلاً المثلث الحاد هـ د و، تكونُ فيّه قِياس الزاوية هـ د وفيه يساوي 50 درجة، وقياس الزاوية د هـ ويساوي 81 درجة، وقياس الزاوية و د هـ يساوي 49 درجة.
• المثلث منفرج الزاوية: هوَ المثلث الذي يكونُ فيّه قياس زاوية واحدة أكبرُ من 90 درجة، مثلاً المثلث المنفرج هـ د و، تكونُ فيّه قِياس الزاوية هـ د وفيه يساوي 120 درجة، وقياس الزاوية د هـ ويساوي 30 درجة، وقياس الزاوية و د هـ يساوي 30 درجة.
• المثلث قائم الزاوية: هوَ المثلث الذي يكونُ فيه قياس زاوية واحدة يُساوي 90 درجة، ويكونُ مجموع قيّاس الزاويتين الأُخرتين 90 درجة، مثلاً المثلثُ قائم الزاوية هـ د و، تكونُ فيّه قِياس الزاوية هـ د وفيه يساوي 90 درجة، وقياس الزاوية د هـ ويساوي 50 درجة، وقياس الزاوية و د هـ يساوي 40 درجة.

أنواع المثلثاث من حيث أطوال الأضلاع:

تُقسم المثلثات من حيثُ أطوال الأضلاع إلى الآتّي:

• مثلث متساوي الأضلاع: هوَ المثلث الذي تتساوى فيّه جميعُ أطوال أضلاعهُ، كذلكَ تتساوى فيّه جميع قياسات زواياه.
• مثلث مختلف الأضلاع: هو المثلث الذي تختلفُ فيه جميع قياسات أطوال أضلاعه، وكذلك قياسات زواياه.
• مثلث متساوي الساقين: هو المثلث الذي يتساوى فيه طول ضلعيّن، وبالتالي تتساوى فيّه قياس زاويتين.

شاهد أيضًا: تصف نظرية فيثاغورس العلاقة بين طولي الساقين والوتر في المثلث المنفرج الزاوية

إلى هُنا نكونُ قد وصلنا إلى نهايةِ مقالنا مركز المثلث هو نقطة تلاقي، حيثُ سلطنا الضوءَ على مفهوم المثلث، وخصائصه العامّة، فضلاً عن أنواع المثلثات من حيثُ قياس الزوايا الداخليّة، وأطوال الأضلاع.