الفرق بين المساحة والمحيط

الفرق بين المساحة والمحيط في الرياضيات أمر يجب على كل دارس للرياضيات معرفته، حيث يقسم علم الرياضيات إلى عدد من الفروع الأساسية، ومن أهم هذه الفروع هو فرع الهندسة الفراغية التي تهتم بدراسة الأشكال والمجسمات من حيث المحيط والمساحة والحجم، وفي هذا المقال يهتم موقع المرجع بتعريفنا على كل من المحيط والمساحة من حيث المفهوم العام، بالإضافة إلى بيان الفرق بينهما، ثم التطرّق إلى ذكر القوانين التي يمكن من خلالها حساب كل من محيط ومساحة الشكل الهندسي.

تعريف المحيط

المحيط الهندسي بشكل ما في الرياضيات هو عبارة عن طول الخط الذي يحيط بالشكل من الخارج، ومن أبرز الأمثلة على المحيط الهندسي هو تخيله على أنّه طول السياج المحيط ببستان، أي أنه بشكل عام يمكن حساب محيط أي شكل مضلع عن طريق جمع أطوال أضلاع هذا المضلع.[1]

شاهد أيضًا: ما هو قانون محيط المستطيل ومساحته

تعريف المساحة

المساحة هي عبارة عن المنطقة المحصورة ضمن محيط الشكل ذو البعد الثنائي، أي يمكن التعبير عنها بسطح، بعبارة أخرة هي المنطقة المحصورة بين مجموعة من الخطوط المغلقة، ويتم حسابها بالواحدة المربّعة، حيث أن وحدة قياسها في الجملة الدولية هي المتر المربع (m²).[2]

شاهد أيضًا: الشكل أدناه يمثل علاقة خطية متناسبة بين عدد الكيلومترات التي تقطعها السيارة

الفرق بين المساحة والمحيط

من أجل بيان الفرق بين كل من المساحة والمحيط الهندسي يجب أن نفهم معنى كل منهما، حيث أن المحيط هو عبارة عن مجموع الأطوال اللازمة من أجل تحديد أطراف شكل ثنائي الأبعاد، أما المساحة فهي عبارة عن عدد الوحدات المربعة اللازمة لتغطية الشكل المطلوب حساب مساحته، ويحسب المحيط في الجملة الدولية بالمتر، أما المساحة فتحسب بالمتر المربع، أي أن:

• المساحة هي عبارة عن امتداد الشكل الذي يغطيه من الداخل، والمحيط عبارة عن الحدود الخارجية للشكل.

الفرق بين المساحة والحجم

في سياق متصل مع التعرف على الفرق بين المحيط والمساحة لا بد لنا من ذكر الفرق بين المساحة والحجم، حيث يكمن هذا الفرق في أن المساحة عبارة عن السطح ثنائي الأبعاد، بينما يكون الحجم عبارة عن الفراغ المتواجد بين عدد من السطوح، أي بثلاثة أبعاد، حيث يمكن لمجسمين أن يكون لهما نفس قيمة مساحة السطح لكن قد يختلفان في الحجم.[3]

شاهد أيضًا: ما هو قانون مساحة المثلث

قانون المساحة

توجد عدد من القوانين التي يتم من خلالها حساب المساحة، ويختلف القانون بالاعتماد على الشكل ونوعه وعدد أضلاعه، حيث سنذكر تاليًا عدد من القوانين التي يتم من خلالها حساب مساحة شكل ما، كما أننا سندرج بعض القوانين التي تشمل حالات خاصة لكل شكل.

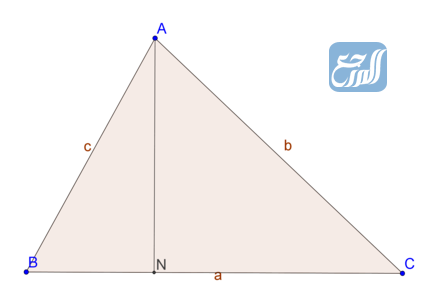
مساحة الشكل الثلاثي

يتم حساب مساحة الأشكال الثلاثية من خلال القانون العام (مساحة المثلث= ½x طول القاعدة x الارتفاع)، حيث يستخدم هذا القانون لجميع المثلثات، ويوجد عدد من القوانين للحالات الخاصة منها نذكر ما يلي:[4]

• مساحة المثلث تساوي نصف جداء طول ضلع في طول الضلع الأخرى مضروبًا في جيب الزاوية بينهما، أي:
  
• مساحة المثلث تساوي جداء أطوال أضلاعه مقسومًا على أربعة أضعاف نصف قطر الدائرة المحيطية المارة برؤوسه، بعبارة أخرى نكتب:
  
• مساحة المثلث القائم تساوي جداء الضلعين القائمتين تقسيم 2.

مساحة الشكل الرباعي

في سياق متصل مع بيان الفرق بين المساحة والمحيط وجب الانتقال إلى مساحة الشكل الرباعي، حيث أن الشكل الرباعي هو الشكل الهندسي الذي يحوي على أربعة أضلاع، ومن أشهر الأشكال الرباعية نذكر ما يلي:

• المربع: وهو عبارة عن الشكل الرباعي المنتظم، ومساحته تعطى بالعلاقة التالية: مساحة المربع= الضلع للتربيع، أو الضلعx الضلع.[5]
• المستطيل: وهو عبارة عن متوازي أضلاع جميع الزوايا فيه قائمة، وتعطى مساحته بالعلاقة: مساحة المستطيل= الطول x العرض.[6]
• متوازي الأضلاع: هو عبارة عن شكل رباعيي غفيه كل ضلعين متقابلين متوازيين ومتساويين، ويكتب قانون مساحة متوازي الأضلاع بالشكل التالي: مساحة متوازي الأضلاع= طول القاعدة x الارتفاع، ويمكن حساب مساحته من خلال معرفة طول ضلعين متجاورين والزاوية المحصورة بينهما من القانون الآتي:[7]
  
• المعين: هو عبارة عن متوازي أضلاع تساوت أطوال أضلاعه وتعامد قطراه، ويمكن حساب مساحة المعين بنفس القانون السابق: مساحة المعين= القاعدة x الارتفاع، كما يوجد قانون خاص به وهو: مساحة المعين= جداء قطري المعين/ 2.[8]
• شبه المنحرف: هو عبارة عن شكل فيه ضلعين متوازيين فقط تسميان القاعدة الصغرى والقاعدة الكبرى، وعلاقة المساحة في شبه المنحرف كما يلي:[9]
  a: القاعدة الكبرى.
  b: القاعدة الصغرى.
  h: ارتفاع شبه المنحرف.

مساحة الشكل الخماسي

الخماسي المنتظم هو الشكل الخماسي الذي تكون جميع أ”وال أضلاعه متساوي، وتحصر بينها زاوية 108 درجات، وتعطى علاقة مساحة الشكل الخماسي المنتظم أو المخمّس باعتبار طول الضلع t كما يلي:

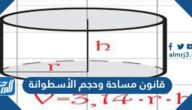
مساحة الدائرة

الدائرة في الهندسة هي عبارة عن مجموعة غير منتهية من النقاط التي تبعد بعدً ثابتًا عن مركز الدائرة O، حيث أن هذه النقاط ترسم حلقة ثنائية البعد، وتسمى كرة في حال كانت بالبعد الثلاثي، ويتم حساب مساحة الدائرة بالاستعانة بنصف القطر r من خلال القانون التالي: مساحة الدائرة= π r²
حيث:  r: نصف قطر الدائرة، π: باي أو ثابت الدائرة الرياضي، ويساوي تقريبًا 3.14، وهو نسبة محيط الدائرة إلى قطرها.[10]

شاهد أيضًا: أنواع المثلثات حسب الاضلاع والزوايا

قانون المحيط

من أجل تمام التعرف على الفرق بين المساحة والمحيط يجب الانتقال إلى السرد الطريقة التي يتم ن خلالها حساب المحيط لكل شكل من الأشكال الهندسية ثنائية الأبعاد، وهذا ما سنتطرّق لشرحه في السطور التالية.

محيط الشكل الثلاثي

محيط المثلث يحسب مثل أي محيط آخر، أي عبارة عن جمع أطوال أضلاعه، أي أننا نكتب: P = a + b + c.

محيط الشكل الرباعي

بشكل عام يمكن حساب محيط الشكل الرباعي من خلال جمع أطوال أضلاعه، كما أنه يوجد بعض القوانين للحالات الخاصّة والتي نذكر منها ما يلي:

• المربع والمعين: المحيط = طول الضلع x عدد الأضلاع.
• متوازي الأضلاع والمستطيل: المحيط = (الطول + العرض)2

محيط الدائرة

من أجل حساب محيط الدائرة نستخدم القانون حيث يُقصد بالحرف r نصف القطر، والعدد باي تعوّض قيمته تقريبيًا 3.14.

شاهد أيضًا:  تم ترتيب ١٠٠ مقعد في حفل مسرحي على شكل مربع . ماعدد المقاعد في كل صف

العلاقة بين المساحة والمحيط

رغم وجود الفرق بين المساحة والمحيط إلا أنه توجد علاقة تربط بينهما، ويمكن من خلال هذه العلاقة أن يتم حساب المساحة باستخدام المحيط، وهي على الأشكال التالية:

• في المثلث: إذا رمزنا لنصف المحيط بالرمز s وأطوال أضلاع المثلث بالرموز a ،b ،c فإن مساحة المثلث تعطى بالعلاقة التالية:
  
• في المستطيل: المساحة = (المحيط x الطول – الطول للتربيع*2)/2

الفرق بين المساحة والمحيط مقالٌ قمنا فيه بذكر التعريف كل من المساحة والمحيط بشكل عام، ثم انتقلنا لبيان الفرق بينهما، بعدها شرحنا بالتفصيل القوانين التي يتم من خلالها حساب كل من المساحة والمحيط لعدد من الأشكال الشهيرة والأكثر استخدامًا بين دارسي الرياضيات، بالإضافة إلى بعض الحالات الخاصة.