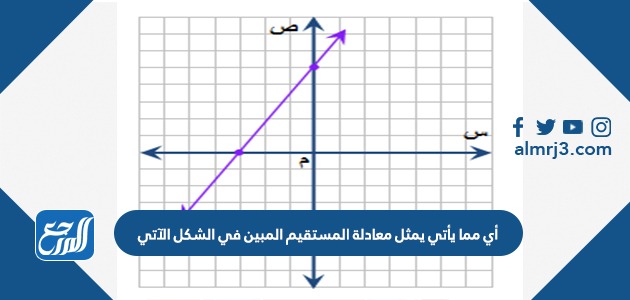
أي مما يأتي يمثل معادلة المستقيم المبين في الشكل الآتي

أي مما يأتي يمثل معادلة المستقيم المبين في الشكل الآتي، يعد علم الرياضيّات من أكثر العلوم التي والت اهتماماً كبيراً من الأشخاص مقارنة مع العلوم الأخرى، فهو من العلوم المتنوعة والموجودة في مجالات عديدة، ولا يمكننا الاستغناء عنها، كما أنها من أساسيات التعليم المهمة في حياتنا، لذا سنوافيكم عبر موقع المرجع الإجابة الكافية حول السؤال المطروح.

المستقيم

يعرف المستطيل على أنه شكل ثنائي الأبعاد، كما أنه رباعي الأضلاع، حيث تكون زواياه قائمة، ومن هذا ينبع أنّ للشكل الهندسي المستطيل زوجين من الضلعين المتساويين و المتقابلين، ومعنى آخر أنّ المستطيل هو الحالة الخاصة من متوازي أضلاع، حيث تكون زواياه كلها قائمة، كما يعد المربع من الحالات الخاصة التي تكون موجودة في المستطيل، حيث تكون أطوال الأضلاع متساوية، يكون الشكل الرباعي إذا تحققت الشروط التالية:[1]

• إذا تساوت جميع زواياه.
• جميع زواياه قائمة.
• إذا كان طولا قطريه متوازيان ومتساويان.
• المستطيل ABCD و المثلثان، حيث نتجا عندما تم وضع قطر:ABD و CDA المتطابقان.

شاهد أيضًا: ما حجم المنشور الرباعي في الرسم أدناه بوحدة سم٣

أي مما يأتي يمثل معادلة المستقيم المبين في الشكل الآتي

تختلف المعادلات الحسابية في علم الرياضيّات، حيث يجد البعض صعوبة بالغة في معرفة الجواب الصحيح لها وإيجاد الطرق التي تؤدي إلى نتائج ممكنة، لذا سنجيب على السؤال التالي:

أي مما يأتي يُمثل معادلة المُستقيم المبين في الشكل الآتي:

• ص = 3_×2
• ص = 2_×2
• ص = 1_×2
• ص = 4_×2
• والإجابة الصحيحة هي: a: ص = 3_×2

شاهد أيضًا: يريد خالد وضع سياج حول حديقة مستطيلة بُعداها ٦ م ٤ م فكم متراً من السياج يحتاج

ما هي خواص المستطيل

يُسمى الضلع الأطول لدى المستطيل بالطول، ويُسمى الضلع الأقصر العرض، حيث تكون مساحة المستطيل هي حاصل ضرب الطول في العرض، كما تكون كافة الزوايا قائمة، وكل ضلعين فيه متقابلين متساويين ومتوازيين، وذلك لأنّه يعتبر نوع خاص من متوازي الأضلاع، بالإضافة إلى أن أقطاره متساوية الطول، ويحتوي المستطيل على محاور تناظر، وكل منهما مستقيم، حيث يمر من منتصفي الضلعين المتقابلين.

وفي ختام مقالنا هذا نكون قد وضحنا فيه جواب السؤال المطروح أي مما يأتي يمثل معادلة المستقيم المبين في الشكل الآتي، كما ذكرنا فيه نبذة عن المستقيم وما هي خواصه.