امثلة على خاصية الابدال

امثلة على خاصية الابدال شاملة، فخاصية الإبدال هي خاصية رياضية تطبق على اثنين من العمليات الحسابية الأربع (الضرب والقسمة والجمع والطرح)، وتطبق هذه الخاصية على الجمع والضرب فقط، من هذا المنطلق سوف نسلط لكم الضوء من خلال سطورنا التالية في موقع المرجع ما هي هذه الخاصية، ونرفق لكم بعض الأمثلة عليها، وتاريخ هذه الخاصية، ولماذا القسمة والطرح ليست عملية غير تبديلية وخصائص عمليتي الضرب والجمع.

ما هي خاصية الإبدال

خاصية الإبدال هي إحدى خصائص الرياضيات القائمة على إبدال أرقام العملية الحسابية، وهذه الخاصية من الخصائص الرئيسية على الأعداد الصحيحة، وتقام على عمليتين من العمليات الحسابية وهما الضرب والجمع، وتمكن هذه الخاصية من إبدال أرقام العملية الحسابية من دون إحداث أي تغيير في الناتج، وصيغة هذه الخاصية تعطى على الشكل التالي: a+b=c ومنه b+a=c، a×b=c ومنه b×a=c.  

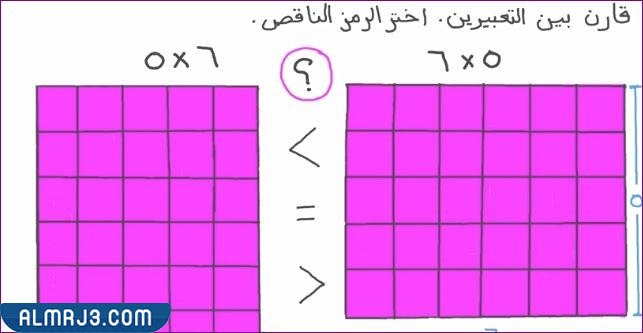
شاهد أيضًا: 8 8 6 تسمى هذه الخاصية بخاصية العنصر المحايد التجميع الابدال التوزيع

امثلة على خاصية الابدال

تشمل الأمثلة على خاصية الإبدال اثنين من العمليات الحسابية، هما عمليتي الضرب والجمع، إليك أمثلة على كل منها:

أمثلة على خاصية الإبدال في الجمع

تقوم خاصية الإبدال على صيغة a+b=c ومنه b+a=c، وهذا لأن الجمع عملية تبديلية، ولأن تبديل موقع كل من الأرقام المجموعة، لا يغير الناتج، ومن الأمثلة عليها:

• 3+4=7 و 4+3=7.
• 5+2=7 و 2+5=7.
• 6+1=7 و 6+1=7.
• 2+4=6 و 2+4=6.
• 2 + 3 = 3 + 2 = 5
• 5 + 10 = 10 + 5 = 15

أمثلة على خاصية الإبدال في الضرب

تقوم خاصية الإبدال على صيغة a×b=c ومنه b×a=c، وهذا لأن الضرب عملية تبديلية، ولأن تبديل موقع كل من الأرقام المضروبة، لا يغير الناتج، ومن الأمثلة عليها:

• 3×4=12 و 4×3=12.
• 5×2=10 و 2×5=10.
• 6×1=6 و 6×1=6.
• 2×4=8 و 2×4=8.
• 5 × 10 = 10 × 5 = 50.
• 2 × 3 = 3 × 2 = 6.

لماذا القسمة والطرح ليست عملية غير تبديلية

إن عمليتي القسمة والضرب ليستا من ضمن العمليات الحسابية التبديلية، وهذا لإن عند قسمة a÷b يشترط أن تكون a> b هذا يعني لا يجوز الإبدال بين مواقع كل منها، لأن الناتج سوف يكون عدد غير صحيح، ولا يكون نواتج كل منهما متساوي، وكذلك الأمر بالنسبة للطرح، عندما نطرح a-b يجب أن يكون a> b وليس العكس، إذاً لنفس السبب القسمة والطرح ليستا ضمن العمليات التبديلية، وهذا نحو الأمثلة التالية:

• 20÷5=4 لكن 5÷20 لا يساوي 4.
• 13- 5=8 لكن 5- 13 لا يساوي 8.

تاريخ ظهور خاصية الإبدال

كان الاستخدام الرسمي للخاصية التبادلية في نهاية القرن الثامن عشر، مع ذلك توجد بعض المعلومات أن هذه الخاصية كانت تستخدم قبل ذلك، وكلمة Commutative والتي تعني خاصية الإبدال هي كلمة فرنسية الأصل، “commute or commuter” مع اللاحقة “ative” والمعنى الحرفي لهذا المصطلح يميل إلى التبديل أو التنقل، ومن القديم هذه الخاصية من خصائص عمليتي الضرب والجمع للأعداد الصحيحة.

خصائص عملية الضرب

لضرب الأرقام الحقيقية عدة خصائص، تشمل هذه الخصائص ما يلي:

• خاصية الهوية: أي أن ناتج ضرب أي عدد بالرقم واحد هو العدد نفسه، وهذا نحو: 7×1=7.
• خاصية الإبدال: أي أن ناتج الضرب واحد عند التبديل بين مواضع الأرقام المضروبة، وهذا نحو: 7×2=14 والعكس صحيح 2×7=14.
• خاصية الضرب الصفري: أي ناتج ضرب أي رقم بالرقم 0 هو 0 مهما كان الرقم، 1765×0=0.
• خاصية الملكية: أي عند ضرب ثلاث أرقام ببعضها البعض ووضع الأقواس يكون ناتج الضرب واحد، وهذا نحو: (3×4) ×5=3× (4×5) =60.
• التوزيع: يمكن توزيع الضرب على الجمع أو الطرح، وهذا نحو: 3× (5+2) =21، (3×5) + (3×2) =21، أو توزيع الضرب على الطرح: 3× (5-2) =9، (3×5) – (3×2) =9.

شاهد أيضًا: هل ناتج ضرب ٥ × ٣٤ هو نفسه ناتج ضرب ٣٤ × ٥ ؟

خصائص عملية الجمع

لجمع الأرقام الحقيقية عدة خصائص، تشمل هذه الخصائص ما يلي:

• خاصية الإبدال: أي أن ناتج الجمع واحد عند التبديل بين مواضع الأرقام المجموعة وهذا نحو: 7+2=9 والعكس صحيح 2+7=9.
• خاصية الملكية: أي عند جمع ثلاث أرقام مع بعضها البعض ووضع الأقواس يكون ناتج الجمع واحد، وهذا نحو: (3+4) +5=3+ (4+5) =12.
• التوزيع: يمكن توزيع الضرب على الجمع، وهذا نحو: 3× (5+2) =21، (3×5) + (3×2) =21.
• خاصية الهوية: وتعني هذه الخاصية ناتج جمع أي رقم مع الرقم صفر والرقم نفسه، وهذا نحو: 5+0=5.

وهكذا نكون قد وصلنا إلى نهاية مقالنا لهذا اليوم الذي كان يحمل عنوان امثلة على خاصية الابدال، وقد أرفقنا من خلاله ما هي خاصية الإبدال، وأمثلة عليها، وتاريخ هذه الخاصية، ولماذا القسمة والطرح ليست عملية غير تبديلية وخصائص عمليتي الضرب والجمع.